1. 自由研究

熱システム

　 電子機器の放熱設計のトレーニングです。ペルチェを使ったデバイスの熱設計などにも使えればと思います。複雑な計算を避けるため、電子部品の熱設計で使われるー熱系ー電機系アナロジで考えます。最後は熱回路網によるシミュレーションを熱回路網のマトリックスを解く手法（参考文献（１）をテキストにして進めます）と電気回路シミュレータを用いて行います。まず用語の整理から始めてみます。やり直し伝熱工学です。
[目次]
１、熱応答を考える
２、用語説明
３、強制対流層流熱伝達　等温平板の場合
４、自然対流熱伝達
５、輻射（熱放射）
６、熱抵坑の種類
７、熱回路網法
８、風を考える
９、非定常問題を考える
例題：ペルチェ冷蔵庫
例題：ペルチェ冷蔵庫を電気回路シミュレータで計算
＜参考文献＞

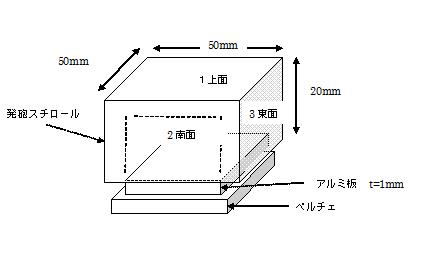
	１、基本式： 熱応答を考えてみます

（１）周辺温度Tiにおかれた物体の温度Toを求めます。たとえば恒温槽温度Tiにおかれた物体の温度応答を求めるイメージです。自然対流の問題です。
　　　
　結論から書きますと
　熱流量 Q = (Ti-To)/RT = CTDT ただしD=d/dt
　ここでＴについて解くと Ti-To = RTCTDT、Ti = (1+RTCTD)To 最終的には
　温度 To = Ti/(1+(RTCT)D) 、To(s)/Ti(s)= 1/(1+(RTCT)s) ただしsはラプラス演算子です
　 　そこでインパルス応答は
　 　｛1/(RTCT)｝/｛1/(RTCT)+s｝を逆ラプラス変換して
　 　
　｛1/(RTCT)｝exp{-t/(RTCT)}となります。--------------（式1-1）
　これは冷却過程の式となります。
　
　ステップ応答は
　｛1/(RTCT)｝/｛1/(RTCT)+s｝{1/s}を逆ラプラス変換して
　
　1 - exp{-t/(RTCT)}となります。-------------------（式1-2）
　これは加熱過程の式となります。
　
　熱時定数RTCT[s] = 物体から周囲への熱抵抗[℃/W]×熱容量[J/℃]
　Dをs(Laplace演算子）に置き換えて、見慣れた１次遅れの伝達関数が見えます。ここまでは１次遅れで表せましたが、サーミスタなどの温度センサーの時定数も考慮すると全体で2次遅れで考えなければならない場合がありますので、注意が必要です。

記号の説明をしますと
　Q = hA(Ti-To) = (Ti-To)/RT
　Q = 熱輸送量(熱流量)[W]=温度差[℃]／熱抵抗[℃/W]
　h = 物体表面の熱伝達率[W/m^2℃]
　A = 物体表面積[m^2]
　To = 物体温度[℃]
　Ti = 物体周辺の温度[℃]
　RT = 熱抵抗 =1/(表面積×熱伝達率)
　dT/dt = 物体の温度変化率
　 　Q = McdT/dt = CTDT
　ここでDは見慣れないかもしれませんがD=d/dtで微分演算子です。D=s(Laplace演算子)に置き換えればLaplace変換になります。
　 　c=average specific heat of the body
　M=mass
　CT=Mc thermal capacitance熱容量[J/℃] =体積×比熱×比重量
　電気回路を思い出して 　　I=E/R, I=CDE, またはR=1/(Cs)と書いたほうが分かりやすいですね。
　なのでアナロジを考えて　T（温度）→E（電圧）, Q（熱流量）→I（電流）, RT（熱抵抗）→R（抵抗）　,CT（熱容量）→C（キャパシタンス）

　[例題１] 　参考文献１の計算例に載っている値を使ってみます。図のような１００Wのヒーターがあります。ヒーターの温度上昇はどのようになるでしょうか。
　
　Q = 熱輸送量(熱流量)[W]=温度差[℃]／熱抵抗[℃/W]
　熱抵抗 =1/(表面積×熱伝達率)
　
　まとめて 　温度差[℃] = 熱輸送量(熱流量)[W]・熱抵抗[℃/W] = 熱輸送量(熱流量)[W]/(表面積×熱伝達率)
　の式と(式1-2)ステップ応答を使って
　物体の温度Ｔoの時間応答を考えます。物体の時定数を求めれば時間応答がわかります。

　与える温度差は熱輸送量(熱流量)[W]・熱抵抗[℃/W] であるので
　温度応答は[温度差×(式1-2)]となります
　温度上昇 = 熱輸送量(熱流量)[W]・熱抵抗[℃/W]・{1-exp{-t/(RTCT)}}
　 　表面積=0.18[m^2]
　熱伝達率=7.05[W/(m^2℃)] （熱伝達率を求めることが１つのポイントなのですが、ここでは既知とします）
　体積=4.5*10^(-4)[m^3]
　比熱=500J/(kg℃)
　比重量=7500[kg/(m^3)]とすれば
　
　熱抵抗[℃/W]RT=1/(表面積×熱伝達率)=1/(0.18*7.05)
　熱容量[J/℃]CT=体積×比熱×比重量=
　時定数[s]=熱抵抗[℃/W]×熱容量[J/℃]
　
　この計算をexcelを使って行います。
　温度上昇は=100*1/(0.18*7.05)*{1-exp{-t/(0.788*1687.5)}} 、 tは時間
　
　 　

	２、用語： よく使われる用語です

　熱量[J], 1[J]=0.2[cal]
　熱流量[W]=[J/s]
　熱流束[W/m^2]
　熱伝導：熱が物体中を伝わって移動する。
　熱伝導率[W/(m℃)]　物質固有の値がある　物性値
　熱伝達：物体間の熱移動
　熱伝達率[W/(m^2℃)] 個体や流体で性質、状況により変化する（物性値ではない）
　熱抵抗[℃/W]
　比熱[J/(Kg℃)]
　　温度はKであるが、ここでは℃と書いてます。
　熱コンダクタンス
　熱容量
　
　覚えておきたい「無次元量」
　・レイノルズ数Re = 流速*代表長/流体の動粘性係数：
　 管路流路ではRe＜ Re＞で　臨界レイノルズ数
　・ヌッセルト数Nu = 熱伝達率*代表長/流体の熱伝導率　
　・グラフホス数Gr = 流体の体膨張係数*重力加速度*固体面の温度上昇*代表長／(流体の動粘性係数^2)
　 　 熱伝達（自然対流）の大きさを表す無次元量
　・プラントル数Pr = 比熱*粘性係数／熱伝導率
　
　ポイントは、熱伝達率はNuで、流体の流れはRe,で自然対流のように重力の場を無視できない場合はGrで、流体の物性値はPrであらわされるので
　Nu=F1(Re,Gr,Pr)
　となるようです。
　 　　

	３、強制対流層流熱伝達　等温平板の場合

境界層近似
参考文献（４）によると
局所熱伝達率：hx[W/(m^2℃)] = 0.332λPr^(1/3)sqrt(u∞/(νx))=1.924834371*sqrt(u∞/x)
参考文献（１）によると
局所熱伝達率：hx[W/(m^2℃)] = 1.93*sqrt(V/X)
流れの上流のほうが熱伝達が大きくなる
ただし、60℃の場合で下記数値を使う。
(40℃):λ=0.0234=kcal/mhdeg=0.0234/0.85985W/mdeg=0.027214W/(m℃)
(60℃):λ=0.0247=kcal/mhdeg=0.0247/0.85985W/mdeg=0.0287259W/(m℃)
(40℃):ν=6.30*10^(-2)[m^2/h]=1.75*10^(-5)[m^2/s]
(60℃):ν=7.06*10^(-2)[m^2/h]=1.96111*10^(-5)[m^2/s]
(40℃,60℃):Pr=0.71

平均熱伝達率:風速Vの気流を受ける長さLの等温平板の表面の場合
参考文献（４）によると
平均熱伝達率 hm[W/(m^2℃)] = 0.664λPr^(1/3)sqrt(u∞/(νL))=3.849668742*sqrt(u∞/L)
参考文献（１）によると
平均熱伝達率[W/(m^2℃)]=3.86*sqrt(V/L)

　

等温平板以外に等熱流速平板がありますが省略します。
参考文献（６）Excelによる伝熱工学も参考になるかと思います。

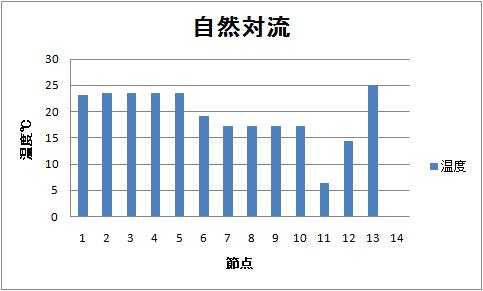
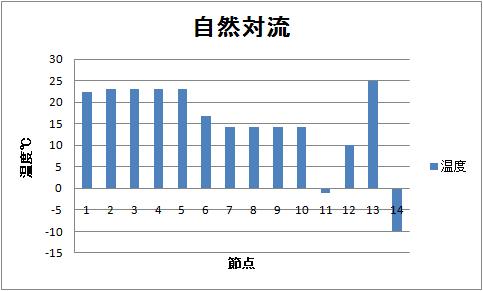
	４、自然対流熱伝達

　壁面の熱流束qw=hx(Tw-T∞) 　局所ヌセルト数Nux=hxx/k, k=熱伝導率,ν=動粘性係数、Pr=プラントル数
自然対流熱伝達の式
　空気・水の場合
　参考文献（４）によると垂直平板自然対流熱伝達は
　・垂直平板　Nu = 0.56(Gr･Pr)^(0.25) ---------------------(式4-1)
ヌッセルト数Nu = 熱伝達率*代表長/流体の熱伝導率であるから　
熱伝達率 hmL = λNu/L = λ0.56(gβL^(3)ΔT/(ν^2)*Pr)^(0.25)/L =λ0.56(gβ/(ν^2)*Pr)^(0.25)･(ΔT/L)^(0.25)
=1.406476778*(ΔT/L)^(0.25) --------------------------------(式4-2)

ここで40℃の場合は
(40℃,60℃):Pr=0.71
グラスホフ数　Gr = gβL^(3)ΔT/(ν^2)
β(体積膨張率)=1/(273+40)
ν(動粘性係数)(40℃):ν=6.30*10^(-2)[m^2/h]=1.75*10^(-5)[m^2/s]
g(重力加速度)=9.8[m/s^2]
λ(熱伝導率)(40℃):λ=0.0234=kcal/mhdeg=0.0234/0.85985W/mdeg=0.027214W/(m℃)
ΔT:温度上昇、L：代表長さ

参考文献（１）によると
熱伝達率[W/(m^2℃)]=2.15*係数Ｃ*（温度差／代表長）^0.25-----(式4-3)
C=0.56とおくと(式4-3)は
熱伝達率[W/(m^2℃)]=1.4056*（温度差／代表長）^0.25----------(式4-4)
となり、(式4-2)と一致する。
参考文献（１）、（６）には対象物の形状と設置条件に対応した係数Cの値が求められていて便利に使えそうである。
　

・水平平板の上面から放熱Nu = 0.54(Gr･Pr)^(0.25)
・水平平板の下面から放熱Nu = 0.27(Gr･Pr)^(0.25)
　・円柱
　・球
などもありますが、詳細は参考文献にありますので、ここまでにしておきます。

	５、輻射（熱放射）

物体の出す熱放射量は、物体の絶対温度の４乗に比例するということで
黒体の輻射能 : Eb = σT^4
物体の熱放射量[W] : E = εEb = εσT^4=放射率*定数*（物体表面の絶対温度[K]）^4
ここで定数σはステファン-ボルツマン定数 = 5.67*10^-8 [W/(m^2K^4)]
εは放射率

放射伝熱量[W/m^2]=係数1*係数2*σ*(T1^-4 - T2^4)

	６、熱抵坑の種類 熱回路網準備

参考文献（４）p30,参考文献（１）p214
熱回路網では対象物を分割して熱抵抗で連結していきます。熱抵抗は伝熱の形態によって異なり、重要なのでまとめておきます。

伝導熱抵抗	R=L/(k･A)	L:伝導経路の長さ[m] ,　k:熱伝導率[W/(m℃)], 　A:伝熱断面積[m^2]
対流熱抵抗	R=1/(h･A)	h:熱伝達率[W/(m^2℃)] , A:放熱面積[m^2]
輻射熱抵抗	R=1/(4εσFA(Tm^3))	ε:輻射率,σ:ステファン・ボルツマン定数[W/(m^2℃)], F:形体係数,A:表面積[m^2],Tm:加熱面と周囲との平均温度[℃]
接触熱抵抗	材料による	サーマルシート0.65℃/W
換気熱抵抗	=温度差／放熱量	=１/（空気の重量質量[Kg/s]・空気の比熱[J/(kg℃)]）

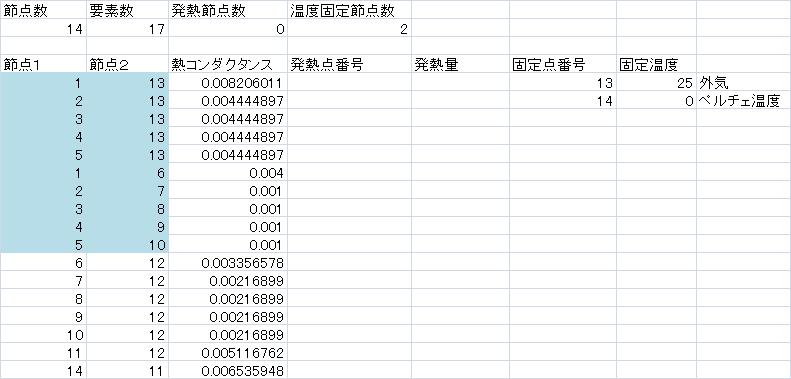
	７、熱回路網法

熱抵抗（熱伝導熱抵抗、対流熱抵抗、輻射熱抵抗）、 熱容量、 キルヒホッフの式、 などの連立方程式を解くことになります。線形方程式は素直に解けそうです（参考文献（１）にサンプルプログラムが掲載されています）が、非線形な場合は繰り返し計算が必要となります（参考文献（４））。
ここで改めて記述することなく、参考文献（７）熱設計なんでも相談室に情報(excelファイル等)がありますので、この辺で留めておきます。実際に問題を解いての注意点は
（１）あらかじめ熱伝達率を仮定して熱回路網で計算します。その後、温度差に応じて熱伝達率の調整が必要です。
（２）ヒートシンクの熱伝達率を設計する時、フィンの影響をどう考えるか。熱伝達率を求める一般式にはフィンの構造を規定したものはありません。計算が複雑になりそうです。ヒートシンク包絡体の体積と熱抵抗の一般的な関係があるようですのでそれが使えます。

８、風を考える

強制空冷を行う場合、圧力損失が発生するということを意識する必要があります。
子供科学館に「ベルヌイのボールが」動体展示がありました。風を受けた（発砲スチロールの）ボールが宙に浮くというもので、見かけた方も多いと思います。

水力学の教科書を広げると、
ベルヌイの定理（流線に沿うエネルギーの式）
p＋γ/(2g)・v^2 ＋γz= 一定 [kgf/m^2] or [kgf・m/m^3] ------------------------(A)

圧力＋{（流体の比重量）／（重力加速度×２）}×流速^2＋圧力損失　＝　一定 -------(B)

（A),(B)を比較すると、γzが圧力損失です。これは位置エネルギーが圧力損失に相当するように書かれていますが、空気の場合の位置エネルギーは考えなくていいとおもいますので、圧力損失としては摩擦による流体抵抗（管路抵抗）、通風抵抗など、あるいは渦に起因するものを考えます
　 　圧力損が発生し圧力差が表示しますので、装置内部で風速が変わるということを意識して放熱設計が必要ということでしょうか。市販の熱設計プログラムがどのようになっているか、気になるところです。
　

９、非定常問題の解法を考える

参考文献（１）には非定常問題の記述（サンプルプログラム）がありません。時間応答を考えたいときは熱容量を含んだ熱回路網を解くことになりますが、気になるところです。
　 回路シミュレータPSpiceやLTspiceなどを使って計算すれば、熱応答も簡単にできそうですので、次の例題で考えてみます。

例題１：ペルチェ冷蔵庫

発砲スチロールのクラーBOXをペルチェで冷却する場合を考えます。ペルチェで部品を冷却する場合が当てはまりま。
計算は参考文献（１）に記載されている熱回路網解析プログラムを用います。
　
　 発砲スチロールの熱伝導率=0.025W/(m℃）、アルミの熱伝導率=170W/(m℃）
　 大きさは、図のように超ミニです。電子部品の冷却程度にしか使えません。
　 　 節点番号 節点位置は
　 1 上面外中央
　 2 南面外中央
　 3 東面外中央
　 4 北面外中央
　 5 西面外中央
　 6 上面内中央
　 7 南面内中央
　 8 東面内中央
　 9 北面内中央
　 10 西面内中央
　 11 アルミ板中央
　 12 内部空気
　 13 外部空気
　 14 アルミペルチェ面

　 設定は下記になります。各面間の相互熱伝導は無視しています。断熱材なのでこの考えが成り立ちます。
　
　 事前に熱コンダクタンスタを計算するのはちょっと厄介ですが、後はプログラムが計算してくれます。
　 ・例えば各面から外気への対流熱コンダクタンス＝表面積*熱伝達率
　 熱伝達率h=2.51*C*(温度差／代表長)^0.25
　 です。Cおよび代表長は面の配置（水平配置か垂直配置か）で異なります。参考文献（6）に詳細があります。

　 また発砲スチロール各面の内面ー外面間の熱抵抗は伝導熱抵抗となります
　 熱抵抗＝（板厚）／（面積×熱伝導率）
　 熱コンダクタンスは１／熱抵抗です。
　 計算結果は下記になります。ペルチェは吸熱量を設定するのではなく、温度を０℃で設定しています。
　 ペルチェ温度を０℃とするとアルミ板の表面温度は6.3℃、内部空気温度は14.3℃になります。
　
　
　 次にペルチェ温度を-10℃にすると、アルミ板の温度は-1.1℃、内部空気温度は10.8℃になります. 　
　 　
　
　 ついでに、強制対流　風速1m/s場合を考えてみます。下記になります。ペルチェ温度を０℃に設定すると、アルミ板は9.7℃　、内部空気温度は12.9℃　であり、内部温度が一様になっている様子です（先述の自然対流に比べて)
　 　

例題2：ペルチェ冷蔵庫、回路シミュレータでの計算

例題１を解くには参考文献（１）のプログラムが必要ですが、ここでは一般的な回路シミュレータ(PSpice等,LTspiceなど）を使って解いてみます。トラ技2005年10月号付録のOrCADを使ってみました。
温度（T)->電圧（V)
熱抵抗（Rt）->抵抗(R) (熱コンダクタンスの逆数)
ここでは使いませんが
　熱容量(Ct)->容量(C)、熱流量（Q)->電流(I)の関係がありますので、熱応答を計算するのは非常に助かりそうです
回路図は

回路は抵抗（熱抵抗）と電源（温度）だけです。runすると回路図に電圧（温度に相当）が書き込まれます。
自然対流の場合の値と同じであることが分かります。

参考文献
（１）国峰尚樹「熱設計完全入門」日刊工業新聞社　１９９７年
（２）内田秀雄編「伝熱工学」裳華房
（３）FRANCIS H.RAVEN "AUTOMATIC CONTROL ENGINEERING" McGRAW-HILL
（４）「エレクトロニクス分野における熱制御　放熱・冷却技術」上下巻　技術情報協会
（５）新潟大学工学部 化学工学資料のページ
（６）Excelによる伝熱工学
（７）熱設計なんでも相談室