1. 自由研究に戻る
  2. Menu表示

横浜から
2011.1．7 横浜、都筑区からみた富士山

Wavelet変換、Wavelet-OFDMの学習

　Wavelet変換については多くの参考文献がありますので、ここでは参考文献（２）に目を通しながら、応用例としてノイズキャンセルとWavelet-OFDMに触れながら学習していきます。Wavelet変換の計算は参考サイト（４）にOctaveのWavelet関数が紹介されていましたので使わせてもらいました、感謝します。（他のサイトにもプログラムは紹介されています。例えば参考文献（２）、（５）などあります。）


wavelet変換の応用例
・JPEG2000--DCTの代わりに使われているらしい
・心電図ウェーブレットから、非浸襲性手法で、心筋梗塞、不整脈の解析
・wavelet-OFDM

Wavelet変換、Wavelet解析

 連続ウェーブレット変換
　任意の信号f(x)とウェーブレット関数Ψa,b(x)との内積
　W(a,b)=＜f(x),Ψa,b(x)＞　を（連続）ウェーブレット変換という。
　　ウェーブレット関数は一般的に複素数であり、内積には複素共役が用いられます。
ここで
　　　基本ウェーブレットΨ(t)
　　　ウェーブレット関数Ψa,b(t)=(1/sqrt(a))Ψ((t-b)/a）
　　　aはスケール（ウェーブレット関数の時間幅,1/aは周波数に相当する）、bは平行移動量
　
離散ウェーブレット変換
　ウェーブレット関数は
　　　Ψj,k(x)=sqrt(2j)Ψ(2jx-k)
　　ここで、N個のサンプリングデータから離散信号ｆ[n]に対する離散ウェーブレット変換を考えてみます。
　　ウェーブレット関数は、
　　　Ψj,k[n]=sqrt(2j)Ψ(2nj-k)　　　ただしN=2M(M:整数)

　離散ウェーブレット変換
　　　W[j,k]=Σnf[n]Ψ*j,k[n]　　(n=0～N-1)
　　　離散信号f(n)と離散ウェーブレットΨ*j,k[n] との内積

　離散ウェーブレット係数
　　　W[j,k]は離散ウェーブレット係数と呼ばれる。

　離散ウェーブレット逆変換
　　　逆変換が存在し、元の信号を再構成できる。（逆変換存在の条件は参考文献２参照）
　　　f[n]=Σj,kW[j,k]Ψj,k[n]

サブバンド分解合成

 分解アルゴリズム
　１つ上のレベルのスケーリング係数　　から新しいスケーリング係数　　とウェーブレット係数　を求める操作。
一般化すると
　cj,m=Σkgkcj+1,2m+k
　dj,m=Σkhkcj+1,2m+k
再構成アルゴリズム
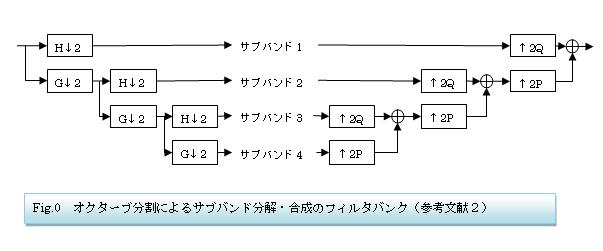
　フィルタバンク
　cj+1,m=Σk{pm-2kcj,k + qm-2kd}
ウェーブレット変換とサブバンド分解
「ウェーブレット変換は、ミラーフィルタの性質を持つ低域通過フィルタと高域通過フィルタをペアとして用い、低域側の信号を次々と2分割する作業を繰り返すことによって行われるサブバンド分解に等価」--- オクターブ分割と呼ばれる。
ここで、後ほど信号のノイズ除去を行う際に必要な「オクターブ分割によるサブバンド分解・合成フィルタバンク」の図が必要です。参考文献（２）P197に載っています。次の図です。
図ではサブバンド４までを表示してますが、後で示す例題ではサブバンド６まで分解しています。
フィルタバンク

ドベシィのウェーブレット

 　ドベシィのフィルタ係数
　q k=(-1)kp2N-k-1
　g k=p k
　h k=q k

ノイズ除去の確認（サブバンド分解合成による）

 　サブバンド分解、合成してノイズ除去の動作を確認してみます。
　50Hzの主信号と、400Hzのノイズがあり、このノイズを除去するために、ウェーブレット変換でサブバンド分解し、ノイズ成分を除去してからサブバンド合成します。
ノイズを含んだ元の信号
　Fig.1は対象とする信号です。サンプリングタイムは1msecで、samples数は512です。
主信号は100samples(100msec)の範囲に5周期存在するので50Hzの信号です。
　Fig.2は対象とする信号のスペクトラムです。ノイズは400Hzにあります。

サブバンド分解
　Fig.3はサブバンド１の分解したもので、ノイズ成分が表れています。
ダウンサンプリングしてますのでsamples数は256になり、サンプリング周期が2msecになります。
50samples(100msec)内に10周期（100Hz）ほど見える信号はノイズ成分です、サンプリングタイムが低くなっているせいでしょう、400Hzのノイズ成分は低い周波数に見えます（アリアスノイズ）。
　Fig.4はサブバンド２の分解です。どうやら主信号のようです。
さらにダウンサンプリングしていますのでsample数は128になり、サンプリング周期は4msecになります。
40samples(160msec)内に8周期(50Hz)ほどに見えるのもは主信号の様です。

サブバンド分解
　Fig.5はサブバンド３の分解です。主信号成分が表れています。サンプリング周期は8msecになります。
20samples(160msec)内に8周期（50Hz）ほど見えます。
　Fig.6はサブバンド４の分解です。サンプリング周期は16msecとなります。
5samples(80msec)内に1周期（12.5Hz）ほど見えます。これはサンプリング周期が低いため、主信号がアリアスノイズとなって表れています。

サブバンド分解
　Fig.7はサブバンド５の分解です。
　Fig.8はサブバンド６の分解です。
　この2つに低周波成分であって、信号は表れていないようです。



これらを元に、ノイズ除去を試みます。
サブバンド合成、ノイズ除去
　Fig.9はサブバンド合成、サブバンド２をwavelet逆変換します。
　Fig.10はサブバンド１を０にクリアしてサブバンド合成し、ノイズ除去します。
　以下にプログラムを示します。

clear 
#Original Signal
t=0:0.001:0.512; # サンプリング周波数1000Hz
y=sin(2*pi*50*t)+0.5*sin(2*pi*400*t); #50Hzの信号,400Hzのノイズ

figure(1);
subplot(2,1,1)
plot(y(1:512)) 
axis([0, 512, -1.5,  1.5]);
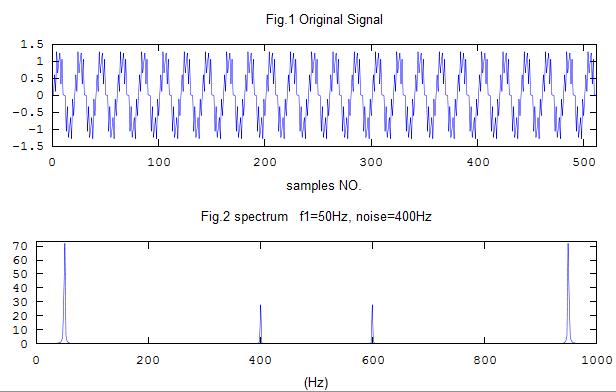
title("Fig.1 Original Signal");  
xlabel("samples NO.")

# FFT表示
Y=fft(y,512); #512フーリエ変換により周波数領域に変換 
Pyy=Y.*conj(Y)/512; # Pyy－スペクトル密度conj－複素共役 
f=1000*(0:511)/512; 

subplot(2,1,2)
plot(f,Pyy(1:512)) 
title("Fig.2 spectrum   f1=50Hz, noise=400Hz")  
xlabel("(Hz)") 
#grid "on";
#------------------------------------------
# -- N = 1 --
#p = [0.707106781 0.707106781];
# -- N = 2 --
p = [0.482962913145 0.836516303738 0.224143868042 -0.129409522551];

sup=length(p); % 数列の長さ
 q = - ( (-1).^(1:sup) ).*p(sup:-1:1); % ドベシイの数列 q_k の生成

g = p;
h = q;
ss=y(1:512);#Origial signal

s1 = dwt1d(ss, g, h);
s2 = dwt1d(s1(1:256), g, h);
s3 = dwt1d(s2(1:128), g, h);
s4 = dwt1d(s3(1:64), g, h);
s5 = dwt1d(s4(1:32), g, h);
s6 = dwt1d(s5(1:16), g, h);
#-----------------------------------------------
#ノイズ除去
is2 = idwt1d(s2, p, q);
iss1(1:256)=is2(1:256);
iss1(256:512)=zeros;
is1 = idwt1d(iss1, p, q);
#----------------------------------------------

figure(2);
subplot(2,1,1);
x=1:256;
plot(x,s1(257:512));
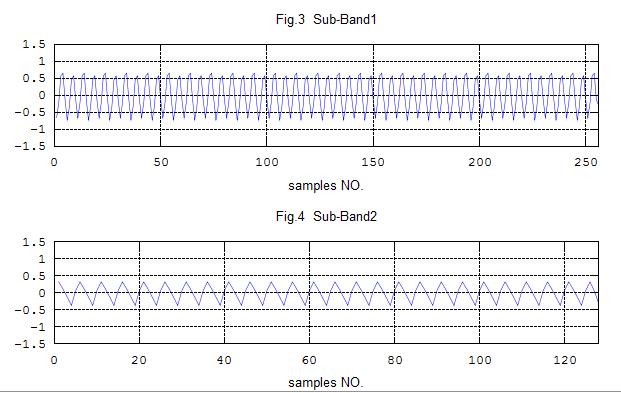
title('Fig.3  Sub-Band1')
axis([0, 256, -1.5,1.5]);
xlabel("samples NO.");
grid "on";

subplot(2,1,2);
x=1:128;
plot(x,s2(129:256));
title('Fig.4  Sub-Band2');
xlabel("samples NO.");
grid "on";
axis([0,128, -1.5,1.5]);

#-----------------------------------------------------
figure(3);
subplot(2,1,1);
x=1:64;
plot(x,s3(65:128));
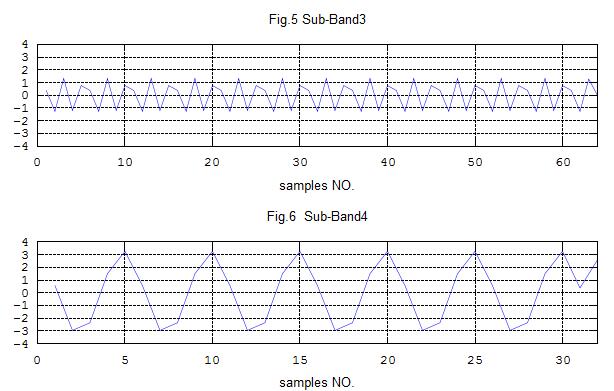
title('Fig.5 Sub-Band3')
axis([0, 64, -4, 4]);
xlabel("samples NO.");
grid "on";

subplot(2,1,2);
x=1:32;
plot(x,s4(33:64));
title('Fig.6  Sub-Band4');
xlabel("samples NO.");
grid "on";
axis([0,32, -4,4]);
#-----------------------------------------------------
figure(4);
subplot(2,1,1);
x=1:16;
plot(x,s5(17:32));
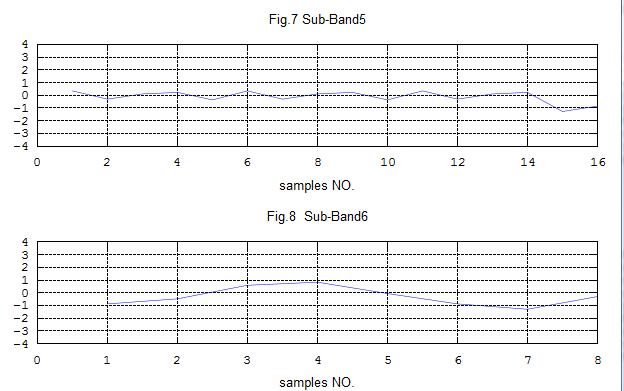
title('Fig.7 Sub-Band5')
xlabel("samples NO.");
axis([0, 16, -4, 4]);

grid "on";
subplot(2,1,2);
x=1:8;
plot(x,s6(9:16));
title('Fig.8  Sub-Band6');
xlabel("samples NO.");
grid "on";
axis([0,8, -4,4]);
#-------------------------------------------
figure(5);
subplot(2,1,1);
plot(is2);
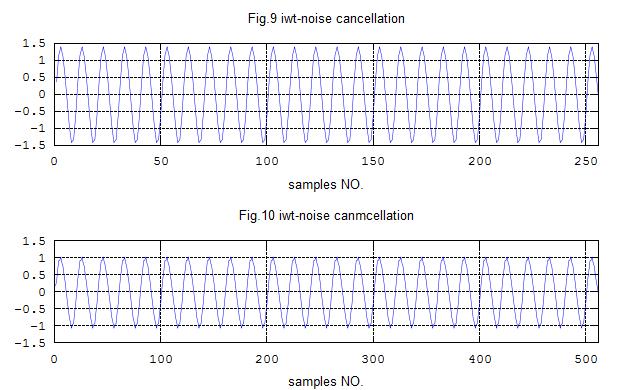
title('Fig.9 iwt-noise cancellation')
axis([0, 256, -1.5,1.5]);
xlabel("samples NO.");
grid "on";

subplot(2,1,2);
%x=1:128;
plot(is1);
title('Fig.10 iwt-noise canmcellation');
xlabel("samples NO.");
grid "on";
axis([0,512, -1.5,1.5]);

#----------------------------------------------------
　 周波数が変化する信号のウェーブレット変換
周波数は変化する信号をウェーブレット変換し、サブバンド分解してどうなるか見てみます。
元の信号
　Fig.11は対象とする信号です。
　Fig.12は対象とする信号のスペクトラムです。ノイズは400Hzにあります。


　Fig.13はサブバンド１の分解です。
　Fig.14はサブバンド２の分解です。

　Fig.15はサブバンド３の分解です。
　Fig.16はサブバンド４の分解です。

　Fig.17はサブバンド５の分解です。
　Fig.18はサブバンド６の分解です。

clear 
t=0:0.001:0.512; # サンプリング周波数1000Hz
ts=1:0.003:2.536;
y=sin(2*pi*50*t.*ts)+0.2*sin(2*pi*400*t); #50Hzの信号,400Hzのノイズ

figure(6);
subplot(2,1,1)
plot(y(1:512)) 
axis([0, 512, -1.5,  1.5]);
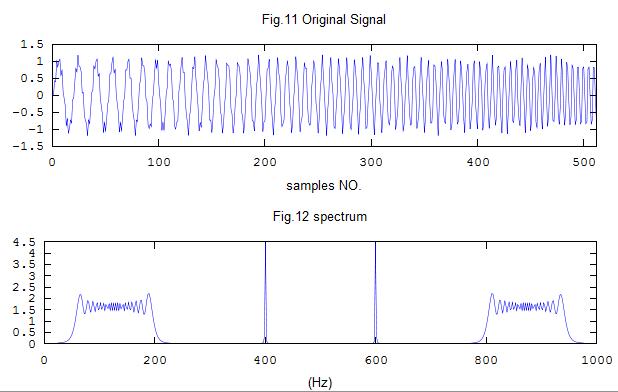
title("Fig.11 Original Signal");  
xlabel("samples NO.")

Y=fft(y,512); #512フーリエ変換により周波数領域に変換 
Pyy=Y.*conj(Y)/512; # Pyy－スペクトル密度conj－複素共役 
f=1000*(0:511)/512; 

subplot(2,1,2)
plot(f,Pyy(1:512)) 
title("Fig.12 spectrum")  
xlabel("(Hz)") 
#grid "on";

#------------------------------------------
# -- N = 1 --
#p = [0.707106781 0.707106781];
# -- N = 2 --
p = [0.482962913145 0.836516303738 0.224143868042 -0.129409522551];

sup=length(p);
q = - ( (-1).^(1:sup) ).*p(sup:-1:1);

g = p;
h = q;

ss=y(1:512); ## Original signal
s1 = dwt1d(ss, g, h);
s2 = dwt1d(s1(1:256), g, h);
s3 = dwt1d(s2(1:128), g, h);
s4 = dwt1d(s3(1:64), g, h);
s5 = dwt1d(s4(1:32), g, h);
s6 = dwt1d(s5(1:16), g, h);
#---------------------------------------------------------------------
figure(7);
subplot(2,1,1);
x=1:256;
plot(x,s1(257:512));
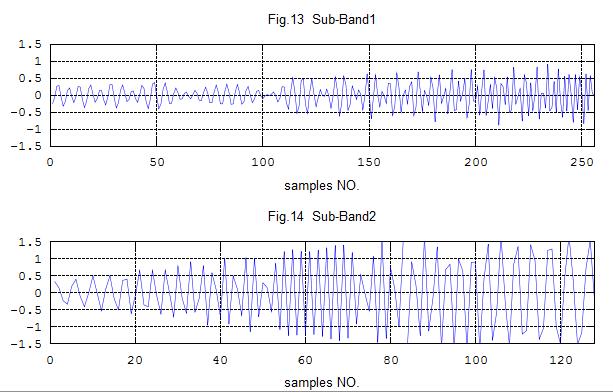
title('Fig.13  Sub-Band1')
axis([0, 256, -1.5,1.5]);
xlabel("samples NO.");
grid "on";

subplot(2,1,2);
x=1:128;
plot(x,s2(129:256));
title('Fig.14  Sub-Band2');
xlabel("samples NO.");
grid "on";
axis([0,128, -1.5,1.5]);

#-----------------------------------------------------
figure(8);
subplot(2,1,1);
x=1:64;
plot(x,s3(65:128));
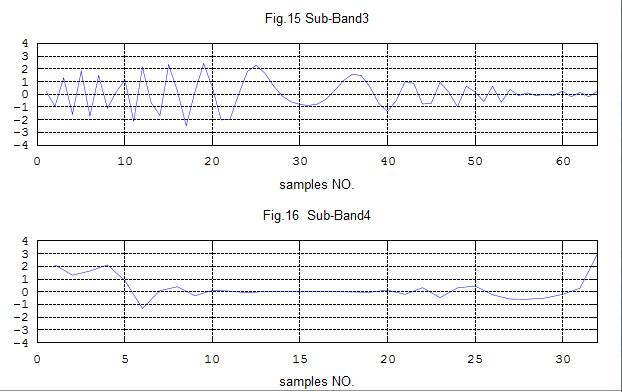
title('Fig.15 Sub-Band3')
axis([0, 64, -4, 4]);
xlabel("samples NO.");
grid "on";
subplot(2,1,2);
x=1:32;
plot(x,s4(33:64));
title('Fig.16  Sub-Band4');
xlabel("samples NO.");
grid "on";
axis([0,32, -4,4]);
#-----------------------------------------------------
figure(9);
subplot(2,1,1);
x=1:16;
plot(x,s5(17:32));
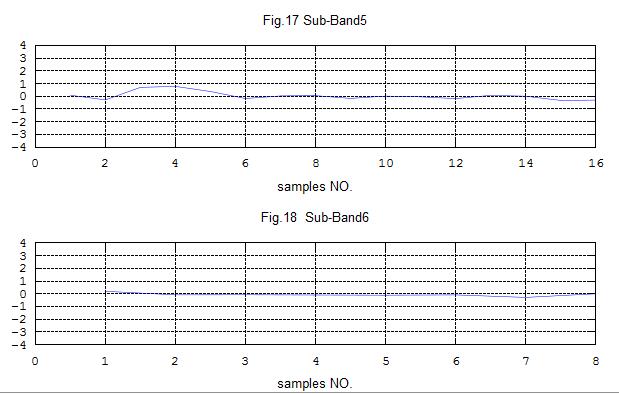
title('Fig.17 Sub-Band5')
xlabel("samples NO.");
axis([0, 16, -4, 4]);
grid "on";
subplot(2,1,2);
x=1:8;
plot(x,s6(9:16));
title('Fig.18  Sub-Band6');
xlabel("samples NO.");
grid "on";
axis([0,8, -4,4]);

Wavelet OFDM

 　Wavelet OFDMらしき動作の確認をOctaveを使ってしてみます。wavelet逆変換とwavelet変換をして、QAMデータが元に戻る事の確認です。参考サイト（４）に紹介されているOctaveのWavelet関数を使います。

送信側
①64QAMデータをシーケンシャルに64個用意する。Fig.1
②それをパラレルデータとして64wavelet逆変換する。－－これは送信されるシリアルデータとなる。Fig.2
受信側
③受信したシリアルデータをwavelet変換する。Fig.3
確認
①＝②となれば確認はおわりです。
　その他の比較確認も（Wavelet OFDMはFFT OFDMに比べてSidelobeが少ない（参考文献５）など）興味ありますが、手に負えそうもありませんのでここまでとします。

送信データ、wavelet逆変換
Fig.1は送信データで64QAMデータを64個用意します。
データは０～６３までシーケンシャルです、青が実部、緑は虚部です。
　M=64;
　data=[0:M-1];
　qamSymbol=qammod(data,M);
Fig.2 はパラレルデータとして一気にwavelet逆変換します。そしてシリアルデータとした信号です。


受信機wavelet変換
Fig.3は受信したシリアルデータをwavelet変換したものです。Fig.1と同じくなっていることから、Wavelet-OFDMはうまくいったとみなします。

64QAM コンステレーション
　 Fig.4はFig.3のwavelet変換したデータをscatterplotしたものです。64QAM信号のコンステレーションが画かれています。 うまく動いているようです。 

#---------------------------------------------------------------------
#   IDWT/DWT OFDMの確認
#---------------------------------------------------------------------
%送信機；データ信号生成 64QAM
M=64;
data=[0:M-1];
qamSymbol=qammod(data,M);
ss=qamSymbol;

# -- N = 1 --
#p = [0.707106781 0.707106781];
# -- N = 2 --
p = [0.482962913145 0.836516303738 0.224143868042 -0.129409522551];

sup=length(p);
q = - ( (-1).^(1:sup) ).*p(sup:-1:1);

g = p;
h = q;

s0 = idwt1d(ss, p, q);% 参考サイト（４）のwavelet逆変換の関数です。
s1 = dwt1d(s0, g, h);%同、wavelet変換の関数です。

#---------------------------------------------------------------------
figure(1);
subplot(2,1,1);
x=0:63;
plot(x,real(ss),x,imag(ss));
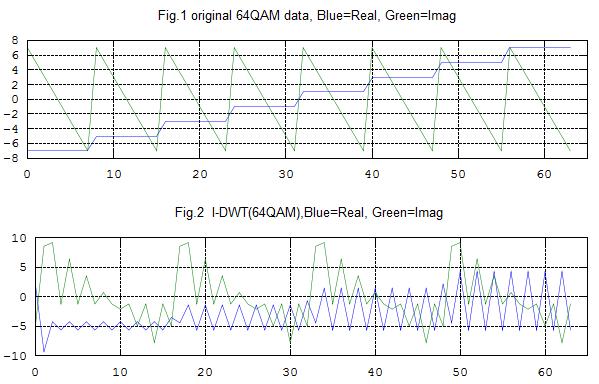
title('Fig.1 original 64QAM data, Blue=Real, Green=Imag')
axis([0, 65, -8,  8]);
grid "on";

subplot(2,1,2);
x=0:63;
plot(x,real(s0),x,imag(s0));
title('Fig.2  I-DWT(64QAM),Blue=Real, Green=Imag ');
grid "on";
axis([0,65, -10,10]);

figure(2);
subplot(2,1,1);
x=0:63;
plot(x,real(s1),x,imag(s1));
axis([-1 1 -2 2])
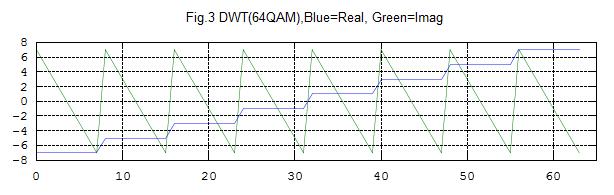
title('Fig.3 DWT(64QAM),Blue=Real, Green=Imag ');
grid "on";
axis([0, 65, -8,  8]);

subplot(2,1,2);
x=0:63;
ifftSS=ifft(ss);
plot(x,real(ifftSS),x,imag(ifftSS));
%axis([-1 1 -2 2])
title('Fig.4 IFFTT(64QAM),Blue=Real, Green=Imag ');
grid "on";
axis([0, 65, -3,  3]);

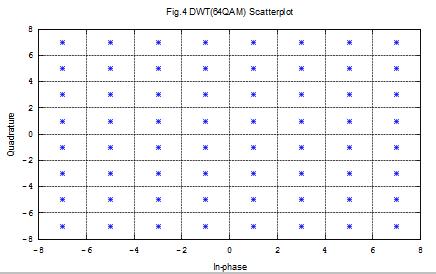
scatterplot(s1,1,0,'b*');
title('Fig.4 DWT(64QAM) Scatterplot');
grid 'on'
参考文献
（１）ウェーブレット解析の計算原理
（２）酒井幸市「ディジタル画像処理の基礎と応用」CQ出版社、2007年改訂版
（３）Wavelet 変換
（４）ウェーブレット変換して遊ぶ
（５）周波数利用効率が非常に高い「Wavelet-OFDM」*注１方式を採用
（６）離散ウェーブレット変換(Wikipedia)
（７）ウェーブレットによる信号処理と画像処理