- 自由研究に戻る
- Menu表示
OctaveでMIMO、アレーアンテナの学習
ディジタル通信システムで使われるMIMO技術をOctave、Matlabを使って学習していきます。OFDMやMIMOは実用化されすでに研究は終了していそうですので、関心のあるところをさらっと基本事項を確認していきたいと思います。
参考文献(1)は自作関数(関数名の頭にMY…として定義されている)がたくさん紹介されて、入門書としてよさそうですので、テキストとして使用しました。その他、多くの参考文献に感謝します。
整合フィルタとは
SN比を最大にするフィルタとして知られている。
どれくらい改善されるかというと、入力信号のSN比をN(Nはサンプル数)倍改善する。
ということです
構造は
トランスバーサルフィルタであって、その重み係数は、信号の自己相関の値となる。
mached filter に詳しく書かれていました。
自由空間および移動通信における伝播損失
参考文献(6)によれば
自由空間における伝送利得G=Pt/Pr={λ/(4*π*d)}^2*Gt*Gr
λ:波長、d:距離, Gt,Gr:送受信アンテナ電力利得
Gt=Gr=1の場合を自由空間伝播利得という。
自由空間伝播損失は距離の2乗に比例する。(距離が2倍になると6dB 減衰する)
移動通信における伝播損失は距離の4乗程度に比例する。
自由空間損失に加え、マルチパスフェージングなどがあり、距離の4乗程度に比例。(距離が2倍になると12dB 減衰する)
レイリー分布する振幅
マルチパスフェージングを受けた受信信号は電力の減衰や波形歪が生じている。その振幅分布の計算モデルは下記の2通りで説明されている。(参考文献6)
・仲上ーライス分布 見通し波など、強い到来波が存在する場合の分布
・レイリー分布 見通し波などの強い到来波が存在しない場合の分布
またレイリー分布は正規分布である、Matlabの関数randnで正規分布の乱数うを発生させて、モデル化することができることが参考文献1に説明されています。
参考文献(4)MATLAB toolboxにはフェージングチャンネルが用意されています。それをオブジェクトとして使用するため下記の関数が用意されています。
rayleighchan関数:
riceianchan関数:
N個の離散的フェージングパスがあり、Nの値により受信信号振幅の振る舞いが異なる。すなわち下記のように定義されています。
N=1の場合は周波数フラットフェージング
N>1の場合は周波数選択性フェージング
なお参考文献(1)ではtoolboxは使わないで標準関数でレイリー分布を計算しています。
周波数選択性フェージング
テキストのP64,【例8】 周波数選択性フェージングをの例を確認してみます。
シミュレーションのための仮定は
平均電力は遅延に対して指数関数的に減衰する仮定をします。
テキストには図が載ってないので、プロット図を書いてみます。
(1)遅延プロファイルの減衰量を10dBにして行ったシミュレーションです。
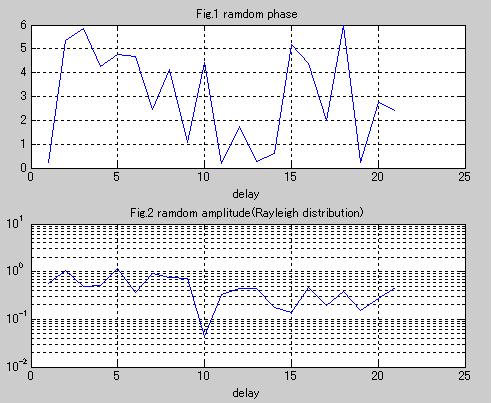
Fig.1は一様分布する位相を表わし、Fig.2はレイリー分布する振幅をしめします。振幅は複素振幅なので、plotはabs関数で大きさ表示しています。遅延100の時に第一到来波に対して10dB減衰する遅延プロファイルです。図のx軸delayは1delayあたり遅延量5に相当します(刻みが5ということ・・分かりずらい)。21delayで減衰量sqrt(10^(-1)/2)になるのは、信号振幅と平均電力の関係みたいです。
この位相と振幅でチャネル応答ベクトルを生成します。
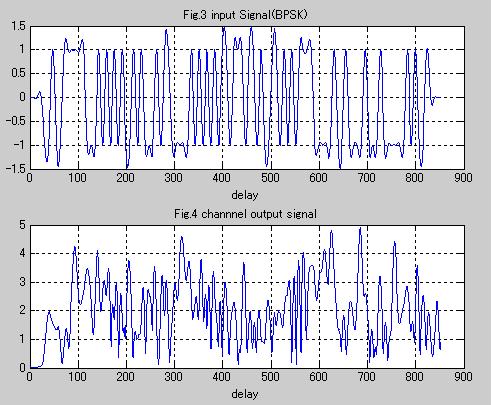
Fig.3は送信信号です。BPSK変調し、ロールオフフィルタを通過させた信号です。
Fig.4はFig.3の信号に遅延を発生させ、先のチャネル応答ベクトルを掛算して作成した、フェージングを受けた信号になります。フェージングの影響を強く受けています。
(2)以下は、遅延プロファイルの減衰量を1000dBにして行ったシミュレーションです。
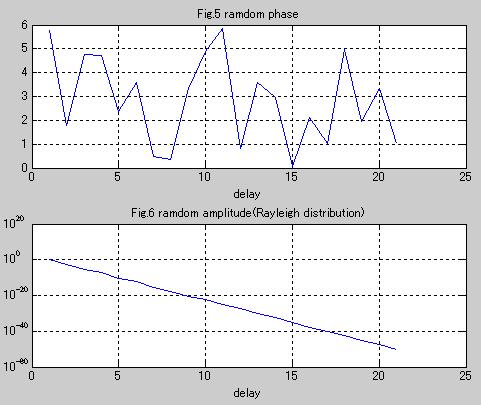
Fig.5はFig.1と同じ。Fig.6は遅延100の時に第一到来波に対して1000dB減衰する遅延プロファイルです。Fig.6のY軸がlogスケールになっていることに注意してください。Fig.2と減衰量が違いおおきな減衰です。delay21付近で減衰量sqrt(10^(-100)/2)になります。
ここのプロットは表示の関係でMatlabを使いました。Octaveではlog scaleのグラフで、y軸のスケールがうまく表示できませんでしたの、やむを得ず使いました。
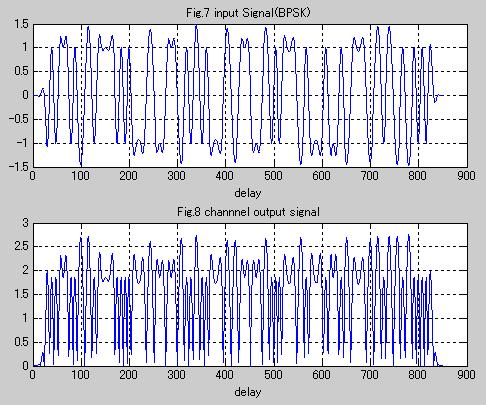
Fig.7はFig.3と同じです。Fig.8はFig.7の信号に遅延を発生させ、チャネル応答ベクトルを掛算して作成した、フェージングを受けた信号になります。Fig.4に比べよりフェージングの影響が少なくなっています。しかしこの信号では受信できるかどうか不安です。
スペクトル拡散とRAKE受信
テキストのP68のスペクトル拡散を確認してみます。
スペクトル拡散は周波数選択性フェージングの影響を軽減するために、先行波と遅延波を完全に分離する手法と言われています。完全に分離後、さらに先行波と遅延波をうまく合成できれば受信信号のSN比を改善できるというアイデアのようです。
また下記事項も重要と思われます。
・チャネル推定:SS(スペクトル拡散)信号を相関器に受信すると、遅延τのみあらず、通信路の位相・振幅を推定できる。
・RAKE合成:相関器によって分離分離されたパス毎のシンボルを合成することをRAKE合成といい、SN比を最大になるように合成するには最大比合成を用いる。
テキストの例題を見てみます。
プログラム例10 SS信号の生成、送信と受信
(未実施)
プログラム例11 RAKE合成のシミュレーション
(未実施)
OFDM
特長は
(1)OFDMは信号をサブキャリアで並列化して送り、トータルでの伝送速度を高くしている。これにより周波数選択性フェージングが起こりずらい。(周波数選択性フェージングは伝送速度が低いほうには影響がないから)
(2)GI(ガードインターバル)を用いて遅延波の影響をなくしている。
(3)スクランブリングと誤り訂正は必要。周波数フラットフェージングに対してはスクランブリングが有効。
(4)位相推定と、同期が必要。サブキャリアごとに受信信号の受信信号の位相回転量は異なる。
(4)の位相回転は、チャネル推定用にM系列信号を埋め込んで、受信信号のM系列部と自己相関をとって検出します。遅延、位相、振幅などを推定することをチャネル推定といいます。
1、OFDM BPSK信号 テキストのプログラム【例12】を確認します。
プログラムソースコードはテキスト(参考文献1)を参照ください。
時間軸で見てみます。データはBPSKです。サブキャリア数128、シンボル数1000、GI長16
QAM信号ではどうなるのかは、後ほど見てみます。
送信機構成は
データ→ 変調(QAM,BPSK等) →チャンネル推定用系列付加 → IFFT → GI付加 → RF信号
受信機構成は
RF信号 → GI除去 → FFT→チャネル系列とデータ系列の分離 →チャンネル推定・位相補償 → データ復調
参考文献(7)のトラ技にもOFDMのシミュレーションがのっています。そちらはExcelを使って、GIの効果を確認しています。
実際にはこの他にも、誤り訂正、インターリーブ等が必要ですが、ここでは触れてません。
(1)送信機:送信データ(BPSK)に、チャネル推定用M系列を付加しIFFTを行い、GIを付加する。
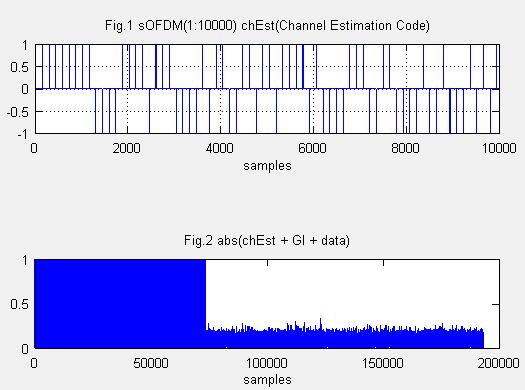
Fig.1は信号の先頭につけた”チャネル推定用系列”のM系列信号です。
Fig.2は変調信号全体ですが、67456サンプルまではチャネル推定用系列が付加され(GI長16×128を含む)、それ以降はデータです。正確なM系列の長さは511×128=65408です。そしてGI長は16×128=2048が先頭につきます。データ長は128×1000=128000ですので 全体で195456です。
(2)周波数選択性フェージング通信路を考える。
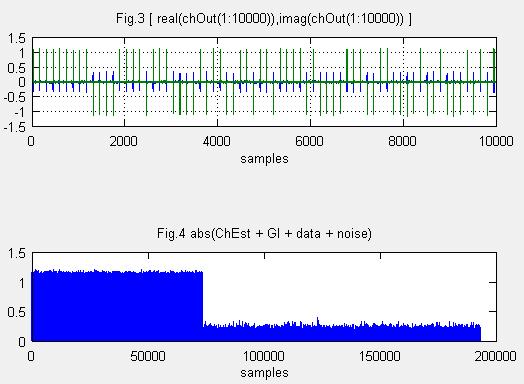
Fig.3,Fig.4はそれぞれFig.1、Fig.2に周波数選択性フェージングと複素ガウスノイズを付加したものです。Fig.3の青色ライン実部の振幅、緑色は位相の振幅を表わしています。I,Q信号に分かれています、BPSKなのでQは0(ゼロ)でもよいのですが、0になってません。
(3)受信機:チャネル推定を行う。
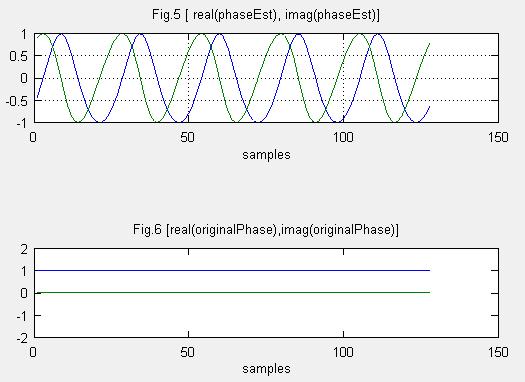
Fig.5は受信した信号から”チャネル推定用系列”を用いてチャネル推定を行った、実部(青色)、虚部(緑)です、位相の回転を意味しています。振幅は正規化していますので振幅は1になってます。
チャネル推定は、受信したM系列と既知のM系列との自己相関を取り求めています。
Fig.6は元データの実部と虚部です。元データも振幅を正規化しているので振幅1で、位相の回転は0です。それが受信信号では位相回転しています。
(4)受信シンボルの位相補償
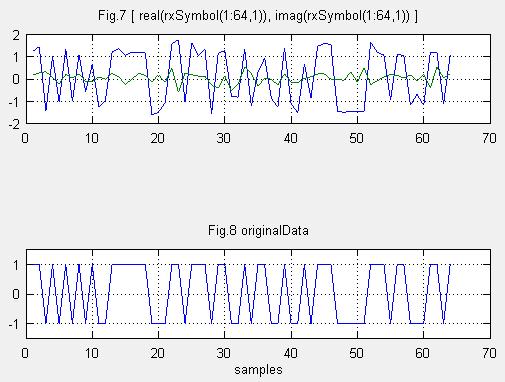
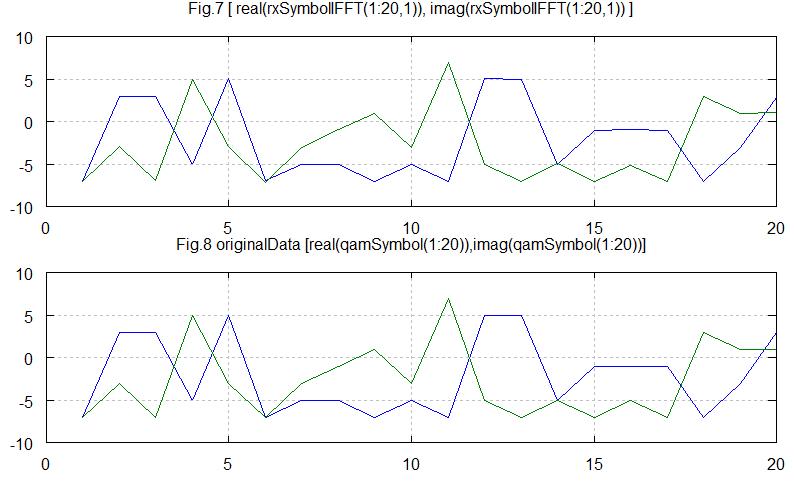
Fig.7は受信した信号です。Fig.8は元データです。送信データはBPSK信号なので、虚部Qは0で実部Iだけが有効です。とすると、受信データは、元データが再現できそうですね。ただし振幅のキャリブレーションを行っていないので、振幅がそろってません。後ほど64QAMデータで振幅補正を行ってみます。
2、それでは64QAM信号の場合を見てみます。
%送信機;データ信号生成 64QAMは
M=64;
data=round(rand(Ns,1)*(M-1)); %整数の乱数を発生させます。64QAMなので0-63までの値をとります。
qamSymbol=qammod(data,M); %64QAM変調です
SPCout=reshape(qamSymbol,Nsub,NofdmSymbol);% S/P変換 です、以降はテキストに沿って行います。
QAMは振幅変調でもあるので、振幅補償が必要です。BPSKの時は位相補償だけ行っていましたが、ここでは両方(振幅と位相)の補償を行います。
(1)送信機:送信データ(64QAM)に、チャネル推定用M系列を付加しIFFTを行い、GIを付加する。
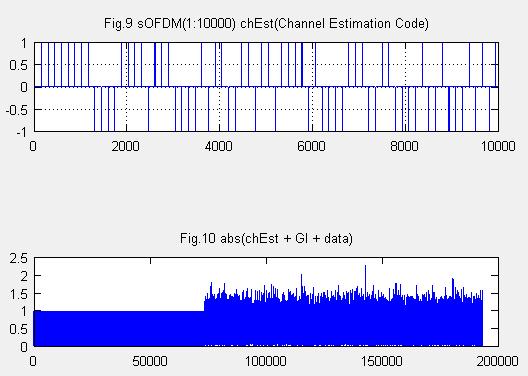
Fig.9は信号の先頭につけた”チャネル推定用系列”のM系列信号です。Fig.10は変調信号全体ですが、67456サンプルまではチャネル推定用系列が付加され(GI(ガードインターバル)を含む)、それ以降はデータです。64QAM信号にしたために、データはチャネル推定用系列信号よりも大きくなってます(振幅が大きくなっている)。
(2)周波数選択性フェージング通信路を考える。
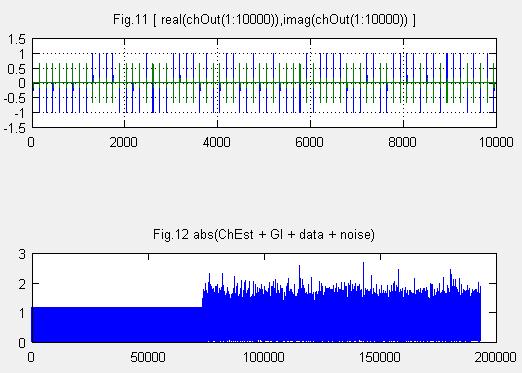
Fig.11,Fig.12はそれぞれFig.9、Fig.10にIFFT後GIを付加し周波数選択性フェージングとノイズを付加したものです。Fig.11の青色ライン実部の振幅、緑色は位相の振幅を表わしています。I,Q信号に分かれています。
(3)受信機:チャネル推定を行う。
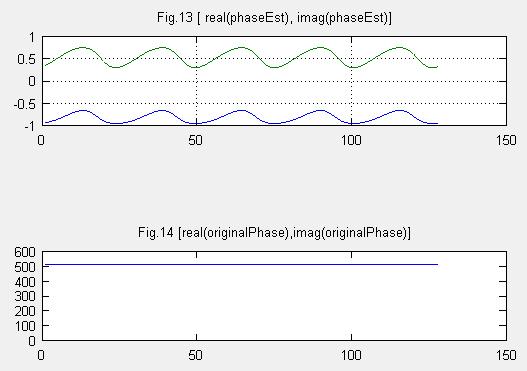
Fig.13は受信した信号から”チャネル推定用系列”を用いて検出した、実部(青色)、虚部(緑)です、位相の回転を意味しています。振幅は正規化しています。
Fig.14は元データの実部と虚部です。元データには振幅は500より大きく、位相の回転は0(グラフでは読み取れませんが)です。受信データ振幅の補正用にこの振幅を使います。受信信号では位相回転しています。
%
%受信シンボルの位相補償とQAMの復調 振幅も補償する
phaseCompMat=phaseEst*ones(1,NofdmSymbol); %位相補償 ここはテキストと同じです。
rxSymbol2=FFTout(:,(seqLength+1:end)).*conj(phaseCompMat); %位相補償された受信信号です
phaseEst3=phaseEst2./phaseOrg; %振幅補償の為 追加します
gainCompMat=phaseEst3*ones(1,NofdmSymbol); %振幅補償 追加します
rxSymbol3=rxSymbol2./abs(gainCompMat);
rxSymbol=round(rxSymbol3);
rxData=qamdemod(MYvec(rxSymbol),M); %振幅および位相の補償がされた受信信号を64QAMで復調します
ここでoctaveで問題が発生しました(matlabはこのままで動きます)
qamdemodを呼び出したときmy_qammod関数がないエラーというエラーです。matlabのwebからこの関数をダウンロードすることで動いてくれました。ただ演算時間はかなり遅く感じました。
(4)受信シンボルの位相補償
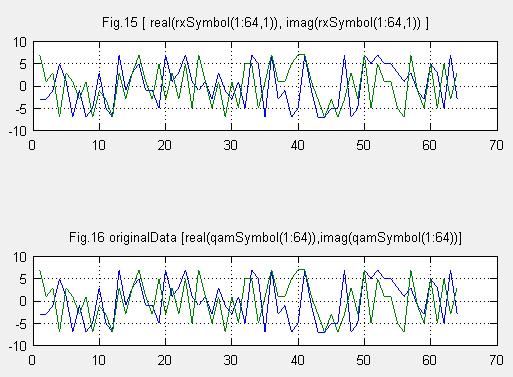
Fig.15は受信した信号の一部です。振幅補正をしたあとです。Fig.16は元データの一部です。目視でも受信信号とも元データは同じよう形に見えます。実際にSN=100dBではビットエラーは発生しなくて、SN=10dBではビットエラーが発生していました。
空間ダイバーシティ
受信側に複数のアンテナを設置して、安定した受信を実現する。受信側で行う空間ダイバーシティには3通り考えられる。
(1)選択ダイバーシティ
複数のアンテナのうち、どれかを選択して使う。
(2)等利得合成
複数のアンテナの位相を合わせて合成する。アンテナの信号強度が落ち込んでいるとSNが劣化する。
(3)最大比合成
位相と振幅を合わせて合成する。SNが最大になるように合成する
送受信モデルを考える。送受信アンテナ間の応答をここではチャンネル応答と呼んでいる。すなわち送受信の伝達関数(チャネル応答)を求め、伝達関数のパラメータを同定する問題に帰着する。
重み係数W(は「複素共役して掛けるもの」と考えておくと後々理解しやすい)
出力 Y[k] = WTX[k]
W=[w1 ; w2 ; ;wn]
最大比合成された信号は、各アンテナのSN比の合計に等しい
・最大比合成重み係数の基本的考え方は2通り
チャネル推定(チャネル応答を用いる)
チャネル応答ベクトルhはそのまま最大比合成重み係数になる
hの共役複素を受信データに掛けるとチャネルの位相回転はキャンセルされる
固有ベクトルを用いる方法
最大比合成の確認
テキストのP107,【例13】 最大比合成の例を確認してみます。
アンテナ数 4
テスト系列長 100
SN 10dB
(1)送信データ作成(BPSK)、通信路:チャネル応答ベクトルの設定して、アンテナ入力信号を作る
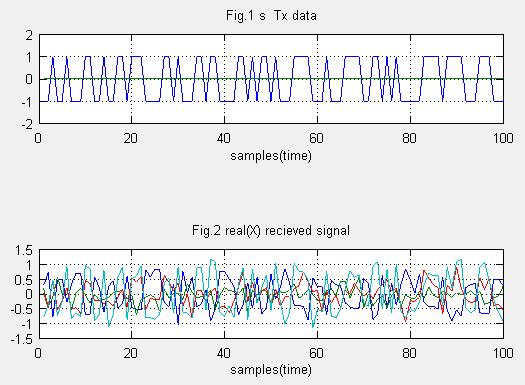
Fig.1はBPSK変調された送信データ(シリアル化されています)
Fig.2はチャネル応答ベクトルを設定し、複素ガウス雑音を付加したアンテナ入力信号です。4アンテナ分プロットされています。
チャネル応答ベクトル:振幅を正規分布に従う乱数で、位相を0〜2πで一様分布する乱数で生成する。ノルムを1にすることで、減衰や増幅を無視しているので出力SNが保存されるということです。
チャンネル応答ベクトルh
送信データs
アンテナの受信信号系列X
X=h*s+複素ガウス雑音
x:最大比重み係数行列
アンテナ出力y=wHX
(2)チャネル推定で最大比合成をおこなう
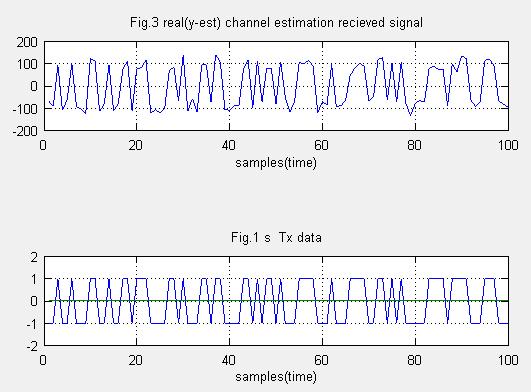
Fig.3はチャネル推定で最大比合成を行い、求めたアンテナ出力です。実部を表示しています。
Fig.4は元データです。よく再現されていることがわかります、テキストではSNで評価しています。
(3)固有値分解で最大比合成をおこなう
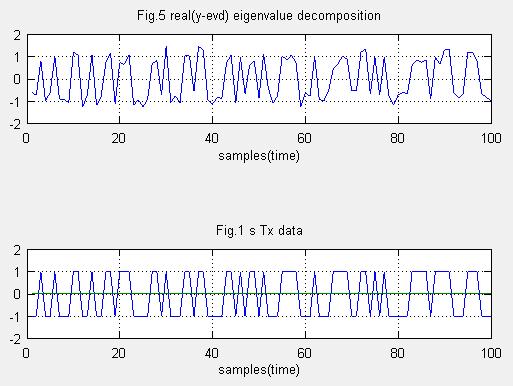
Fig.3は固有値分解で最大比合成を行い、求めたアンテナ出力です。実部を表示しています。
Fig.4は元データです。よく再現されていることがわかります、テキストではSNで評価しています。
SFBC送信ダイバーシティ
テキストから少しずれますが、参考文献(9)を元に、SFBC(space-frequency block coding)という送信ダイバーシティを眺めてみます。2アンテナポートの場合、LTEではSFBCダイバーシティが用いられます。最初のアンテナポートには連続する変調シンボルd(i)とd(i+1)とが互いに隣接するサブキャリアにマッピングされます。第2のアンテナポートには-conj (d(i+1))とconj (d(i))とが同一(最初のアンテナポートと同じという意味)の隣接サブキャリアで送信されます。ただしconj ()は複素共役を表わします。
3GPPでは TS36.211 6.3.3.3及び6.3.4.3でSFBCが定義されて、次のように表わしています。
3GPP TS36.211 6.3.3.3でのlayer mapping
x(0)(i)=d(0)(2i)
x(1)(i)=d(0)(2i+1)
3GPP TS36.211 6.3.4.3でのprecoding
y(0)(2i)=(1/sqrt(2)){Re(x(0)(i) + j Im(x(0)(i)} = S1
y(1)(2i)=(1/sqrt(2)){-Re(x(1)(i) + j Im(x(1)(i)} = -S2*
y(0)(2i+1)=(1/sqrt(2)){Re(x(1)(i) + j Im(x(1)(i)} = S2
y(1)(2i+1)=(1/sqrt(2)){Re(x(0)(i) - j Im(x(0)(i)} = S1*
参考文献(9)P36より
| サブキャリア | アンテナ1 | アンテナ2 |
| 2k | S1 | -S2* |
| 2k+1 | S2 | S1* |
この後は、MRCを用いて受信するようです。
アダプティプアレーアンテナ
空間ダイバーシティは、アンテナを空間的に十分離して設置していました。
アダプティプアレーは、反対にアンテナ間を波長間隔(半波長も含めて)に設置、受信信号に相関をもたせています。アンテナの指向性も構成できます。
受信信号のモデルには下記がポイント
平面波の仮定
経路長差
アンテナ間隔をd、角度θで信号が到来する。ちょうど光学部品の回折格子のような振る舞いをします。
経路長差はdsinθ、位相差はφ= 2π/λ・dsinθ
ステアリングベクトルの導出
steering vector(steerは操縦する、案内するという意味)
X[k]=A(θ)S[k] : X[k]は受信信号ベクトル、A(θ)はステアリングベクトル、S[k]は信号
相関行列
アンテナ素子間の相関特性(コヒーレンス)を行列で表わす。(k,l)成分が素子kと素子lの間の受信信号の相関を表わすようにした行列である。
Rxx=E[X(t)・X(t)H]
E[・]は期待値を意味します。期待値は平均と類義語です。
ウィナーの解
希望信号を取り込みながら、干渉信号を打ち消す。このような重み係数を求めるにはどうすのだろうか。このような状態を完全に解くことは出来ないが、最もよい解をえることは出来る。この解がウィナー解である。
それは評価関数を最小にする、最適制御と同じ考えである。2乗平均誤差を最小にする、2乗誤差最小化(MMSE)基準を満足するような解と同じである。
%ウィーナー解の計算
相関行列Rxx
参照信号ベクトルr
アンテナ入力信号X
ウィーナー解 w=inv(Rxx)*X*conj(r)
X*conj(r)は参照信号と入力信号ベクトルとの間の相関ベクトル
アンテナ出力は y=w'*X
MMSEアダプティブアンテナ
MMSE基準(または規範)のアダプティブアンテナは、受信側で用意する参照信号と実際のアレー出力徒の差を最小にすることによって最適なウェイトを決定する。アダプティブヌルステアリングと同時にアダプティブビームフォーミングを行うことが出来るが、参照信号が必要になる。
・LMS(Least Mean Square)法 --ウィナー解の最適化アルゴリズムの一つ、最急降下法
・SMI(Sample Matrix Inversion)法-- ウィナー解の理論式を直接解く直接解法
・RLS(Recursiv Least Square)法-- SMIのようにサンプル値を用いて相関値を推定、かつウェイトを逐次更新
アンテナ指向性の描画
アンテナ数、波長で正規化したアンテナ間距離、および重み係数が分かれば、アンテナの指向性を調べる事が出来る。
出力SN比の計算法
アダプティブアレーアンテナによって出力SN比は入力SN比のアンテナ数倍大きくなる。ただし干渉波を打ち消すことを同時に行っている場合はそうならない。
逐次的な重み係数うの推定法
LMS法
RLS法
重み係数のブラインド推定
CMA法
ウィナー解に基づくアダプティブアレーアンテナ
テキストのP122,【例14】 ウィナー解に基づくアダプティブアレーアンテナの確認をして見ます
ここでの方法は、直接解法なのでSMI法に当てはまるようです。
設定項目は
希望信号到来角度=-20
干渉信号到来角度=30
アンテナ数=4
アンテナ間隔=0.5
SN
希望到来信号 S(1,:)
干渉到来信号 S(2,:)
参照信号をr=S(1,:)として、wienerの解で重み係数を求めたあとで、その重み係数を用いてデータ信号を受信する。
(1)送信データ(BPSK)および、アンテナ入力信号生成
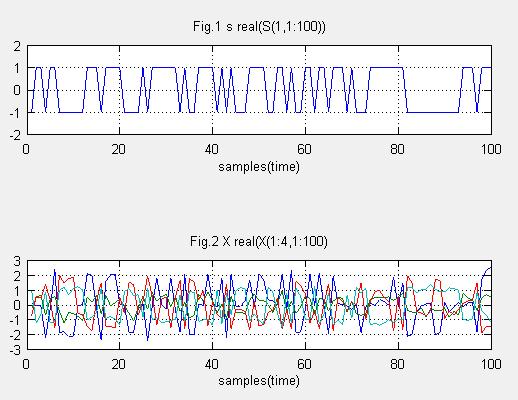
Fig.1 送信データです(BPSK)
Fig.2はステアリングベクトルと複素ガウス雑音を加え、アンテナ入力信号Xを計算する。4アンテナ分をプロット。
(2)ウィーナーの解に基づくアンテナ出力
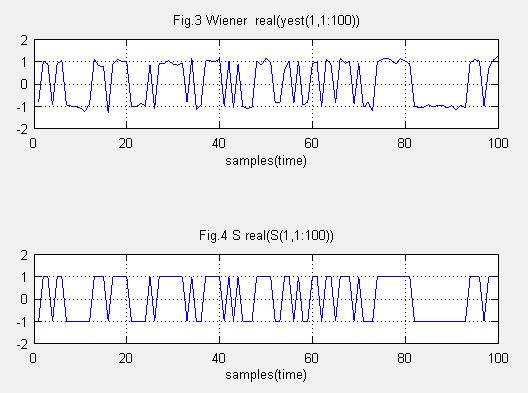
Fig.1はウィーナーの解に基づき重み係数を求め、アンテナ出力信号を生成しています。
Fig.2は元データです。
%ウィーナー解の計算
相関行列Rxx
参照信号ベクトルr
アンテナ入力信号X
ウィーナー解 w=inv(Rxx)*X*conj(r)
アンテナ出力は y=w'*X
入力SNは10dBで出力SNは15.58dBであった。理論的にはアンテナ4本なので6dB高くなる。
それでは
アンテナパターンを見てみます。テキストでは横軸を角度にしていますが、極座標で見てみます。
ただし、アンテナは等間隔で一列に並んでいる場合ですので、並べ方を変えれば違うパターンになるでしょうから注意してください。
Octaveには極座標でのplot関数polarが用意されています
例えば、polar(doa*pi/180,10*log10(P_theta)+50)のように使います
(2−1)アンテナ数4の場合(【例14】本例題の場合)
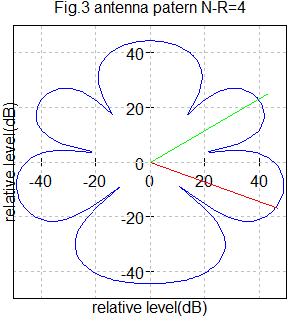
Fig3はアンテナ数4の場合です。
希望信号到来角度=-20(赤色ライン)、干渉信号到来角度=30(緑色ライン)
信号強度は相対値です。-40,-20とか負号がついていますが、Octaveが付けているもので、方向(角度)を意識して描いているのでしょう。信号強度が負なのではありません。
図において水平方向(X軸)の右側は0度、左側が−180度になりますので、4本のアンテナは垂直軸(Y軸)方向に並んでいることになります。4本の各アンテナは、それぞれ図の右半面と左半面対象にアンテナパターンが描かれています。
(2−2)アンテナ数2の場合(【例14】のアンテナ数を2にする)
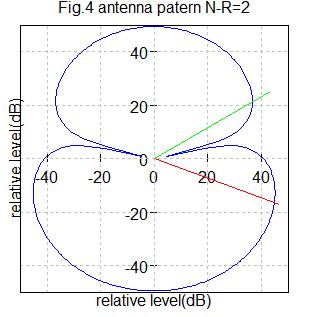
Fig4はアンテナ数2の場合です。
(2−3)アンテナ数8の場合(【例14】のアンテナ数を8にする)
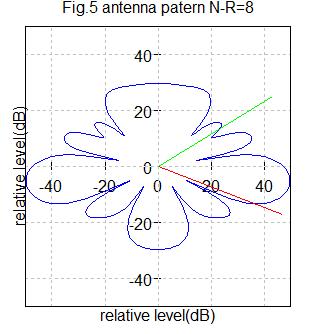
Fig5はアンテナ数8の場合です。
希望信号到来角度=-20度(赤色ライン)、干渉信号到来角度=30度(緑色ライン)
何度かシミュレーションを実行してみますと、うまくいかない(希望波をとらえられない)場合もあるようです。
アンテナを増やせばうまくゆくとも限らないような気がします。
LMS法/RLS法
逐次的な重み係数の推定法としてMMSE基準によって最適解を求めるLMS法とRLS法が紹介されています。
LMS法はサンプルごとに重み係数を更新していきますが、LMS更新式の収束を左右するステップサイズの取り方が難しい。ステップサイズが大きいと収束は早いが不安定になり、小さいと収束は遅いが安定となる。
ここで考えられたのがRLS法で、ステップサイズを適応的に変えていく方法です。
LMS法のアンテナパターン
(3)テキストのプログラム【例15】P124のアンテナパターンを描いてみます。アンテナ数2,4として希望波、干渉波の到来角度を変化させてみてみます。
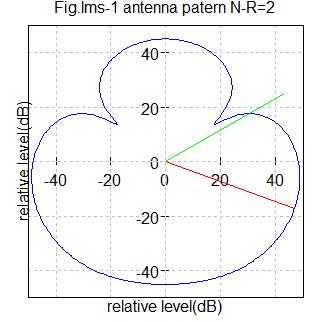
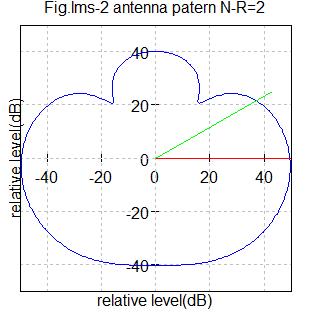
Fig.lms1 アンテナ数2
希望信号到来角度=-20度(赤色ライン)
干渉信号到来角度=30度(緑色ライン)
Fig.lms2 アンテナ数2
希望信号到来角度=0度(赤色ライン)
干渉信号到来角度=30度(緑色ライン)
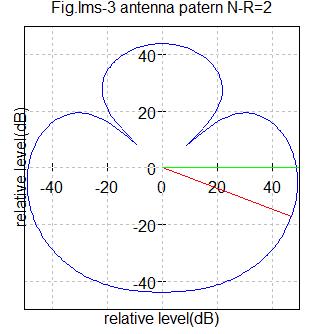
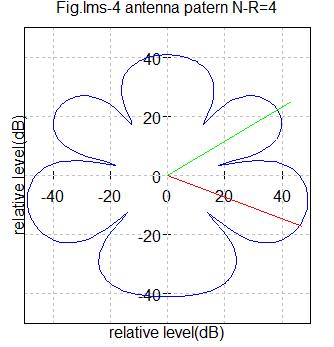
Fig.lms3 アンテナ数2
希望信号到来角度=-20度(赤色ライン)
干渉信号到来角度=0度(緑色ライン)
Fig.lms4 アンテナ数4
希望信号到来角度=-20度(赤色ライン)
干渉信号到来角度=30度(緑色ライン)
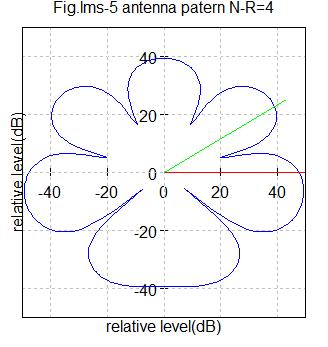
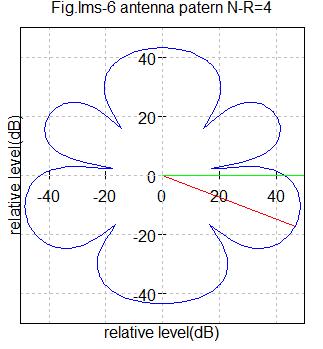
Fig.lms5 アンテナ数4
希望信号到来角度=0度(赤色ライン)
干渉信号到来角度=30度(緑色ライン)
Fig.lms6 アンテナ数4
希望信号到来角度=-20度(赤色ライン)
干渉信号到来角度=0度(緑色ライン)
LMS法のアンテナパターン、干渉信号が2波の場合
プログラム【例141】〜【例16】は干渉波を増やすことが出来ます。
干渉波を2つにしてみます。
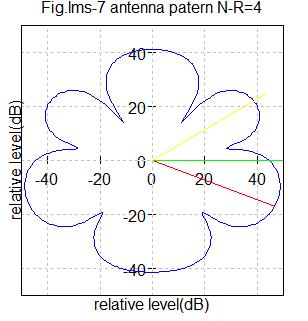
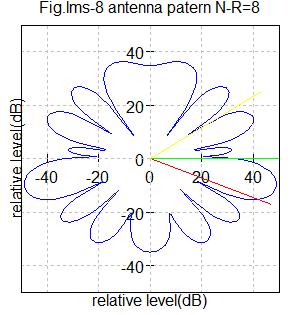
Fig.lms7 アンテナ数4
希望信号到来角度=-20度(赤色ライン)
干渉信号到来角度=0度(緑色ライン)
干渉信号到来角度=30度(黄色ライン)
Fig.lms8 アンテナ数8
希望信号到来角度=-20度(赤色ライン)
干渉信号到来角度=0度(緑色ライン)
RLS法のアンテナパターン
(4)テキストのプログラム【例16】P125のアンテナパターンです。
wiener法、LMS法、RLS法は重み係数を求める方法が違いますが、このシュミレーション条件ではアンテナパターンに大きな違いが見えないようです。
LMS法の場合と同じように希望波の到来角度を変化させたときのアンテナパターンをRLS法の場合に見てみます。先ほどと同じように角度によって”死角”(不得意角度)のようなものがあるようです。(残念ですがこれはアンテナを一列に配置した場合ですのでそれ以外の配置に当てはまるかどうかは議論されていません)
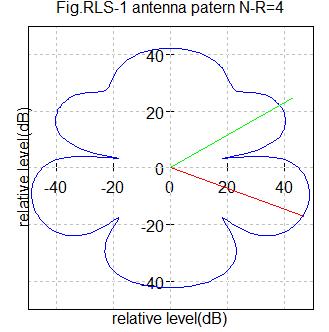
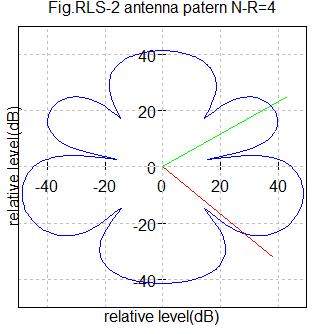
Fig.RLS1 アンテナ数4
希望信号到来角度=-20度(赤色ライン)
干渉信号到来角度=30度(緑色ライン)
Fig.RLS2 アンテナ数4
希望信号到来角度=-40度(赤色ライン)
干渉信号到来角度=30度(緑色ライン)
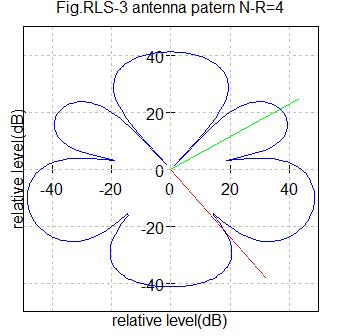
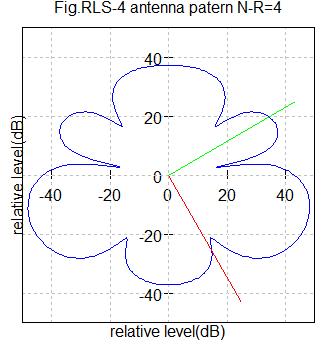
Fig.RLS3 アンテナ数4
希望信号到来角度=-50度(赤色ライン)
干渉信号到来角度=30度(緑色ライン)
Fig.RLS4 アンテナ数4
希望信号到来角度=-60度(赤色ライン)
干渉信号到来角度=30度(緑色ライン)
CMA法を用いてみます
CMA法によるアダプティブアレーアンテナは、参照信号を不要とする重み係数推定法です。
テキストの例17です。
(5)CMA(Constant modulus algorithm)法によるアンテナ出力
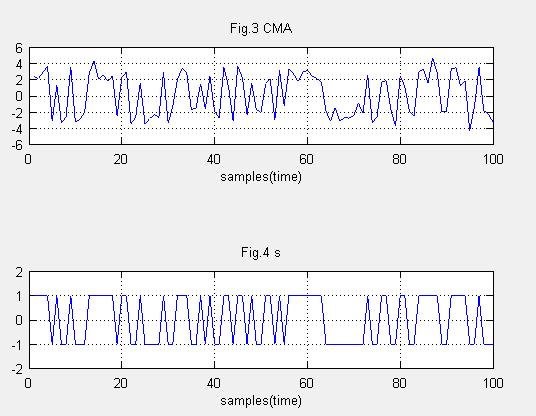
Fig.3CMA法によるアンテナ出力です。
Fig.4は元データです。SNは14.43とwiener法に比べ低い値です。
CMA法は、アダプティブアレーアンテナ出力の包絡線が一定となることを制御基準とする。PSK変調には適用できると言いますが、OFDMには適用できなくなるということでしょう。
MIMO(2×2),特異値分解による方法
送信側にも複数のアンテナを用いることで、マルチパスフェージング環境で通信路容量を増やせる。MIMOも空間ダイバーシティの一つ。
X=H*U+雑音
X=MIMOの受信信号
H=チャネル応答行列
U=送信信号行列
H=MYcompNoise([N_R,N_T],1);%チャネル応答ベクトル 平均電力1の複素正規乱数
[V_R,LambdaM,V_T]=svd(H);%特異値分解
1、特異値分解に基づくマルチモード伝送の例です
テキスト プログラム【例18】の確認です。SNは20dBで計算。
特異値分解では U=VtS:Sは信号行列
アンテナ N_R=2,N_T=2の 2×2MIMO, Ndata=1000,BPSKデータです。
(1)信号系列を作る。ランダムなBPSK信号です。
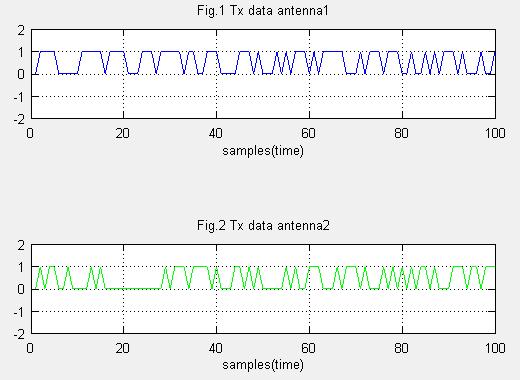
Fig.1はアンテナ1の信号系列です。ランダムデータのBPSK信号です(100シンボルまで表示)
Fig.2はアンテナ2の信号系列です。
(2)送信信号系列を作る。U=V_T*S
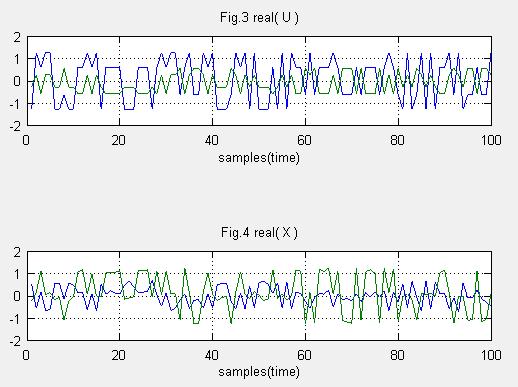
Fig.3,4は信号系列の実部と虚部です。青色:アンテナ1、緑色:アンテナ2です。実部を見ると、アンテナ1の値が平均して大きい。虚部はアンテナ2が大きいように見えます。
(3)受信信号系列Yを求める
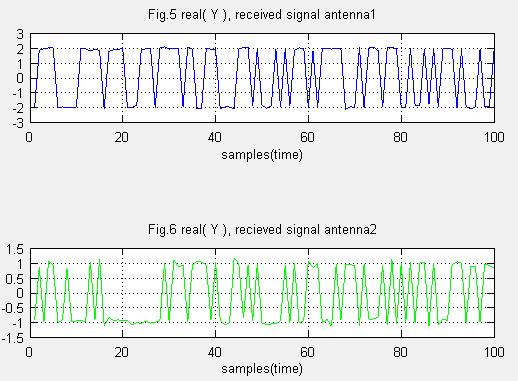
Fig.5,6はアンテナ1と2の受信信号系列です。アンテナ1の信号が2倍の振幅で受信されています。これはMIMOの性質なのでしょうか。テキストには、それぞれの伝送路のSN比は異なるという記述があります。
Y=V_R'*X; %ただし[V_R,LambdaM,V_T]=svd(H);
(4)受信信号系列を復調する。
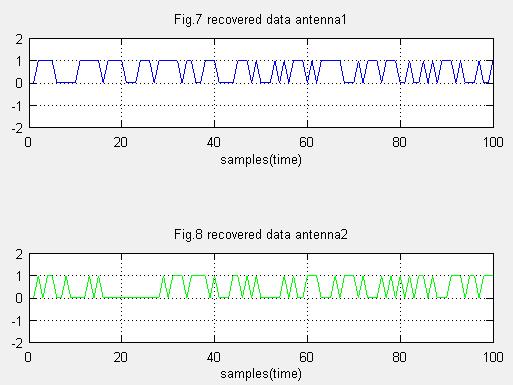
Fig.7,8は復調したデータです。Fig.1,2(下の図)と比較してみます。とりあえず目視比較で、一致していそうです。

次に
2、OFDM-64QAM信号で確認してみます
雰囲気を味わうため、計算を簡単にします。遅延なし、フェージングなし、GIなしで考えてみます。
チャンネル推定様にM系列を先頭に付加します。OFDMの項で確認した内容と同じです。SN40dBを設定。
(遅延とフェージングが無いと位相が回らないようなので、後ほど入れて検討してみます)
(1)M系列を含んだ信号系列を作る アンテナ1
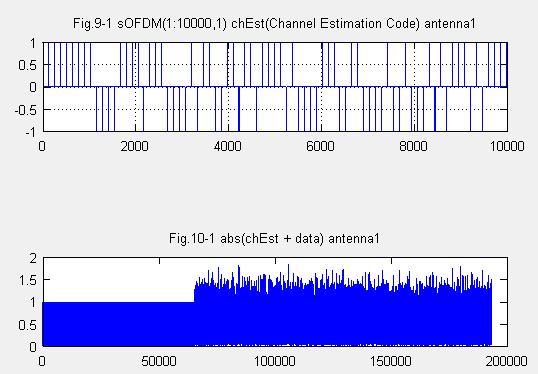
Fig.9-1は信号の先頭につけた”チャネル推定用系列”のM系列信号です。
Fig.10-1は変調信号全体ですが、65408サンプルまではチャネル推定用系列のM系列が付加されています(長さは511×128=65408)、それ以降はデータです。正確な。データ長は128×1000=128000ですので 全体で193408です。
(2)M系列を含んだ信号系列を作る アンテナ2
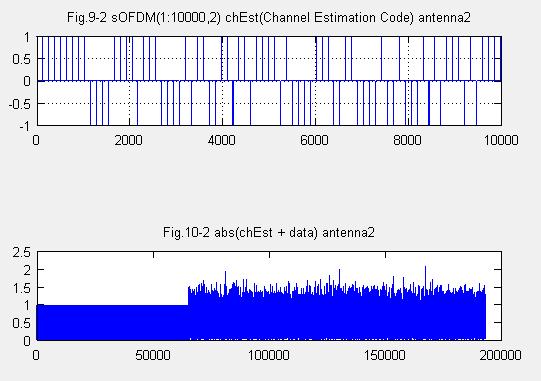
(3)送信信号系列Uを作る アンテナ1と2
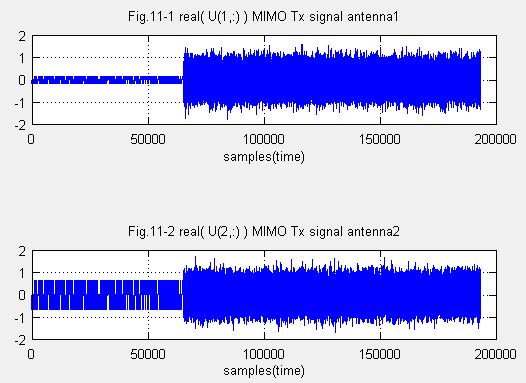
Fig.11-1,11-2は送信信号系列はU=V_T*Sですが、アンテナ1とアンテナ2ではM系列に相当する部分の振幅が異なっています。特異値分解されたV_Tの性質なんでしょうか。?これは特徴のようです。
(4)MIMO受信信号Xを求める アンテナ1と2
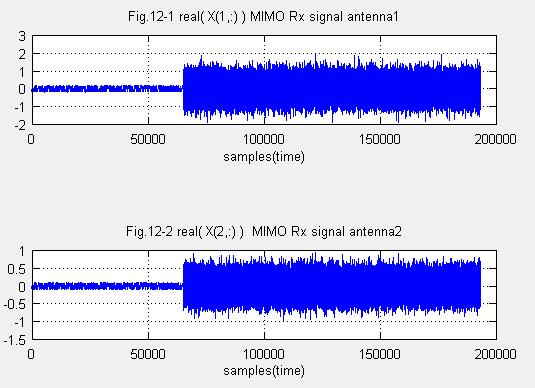
Fig.12-1, 12-2はMIMO受信信号X=H*V_T*S+複素ガウスノイズです。
(5)受信信号行列Yを求める アンテナ1
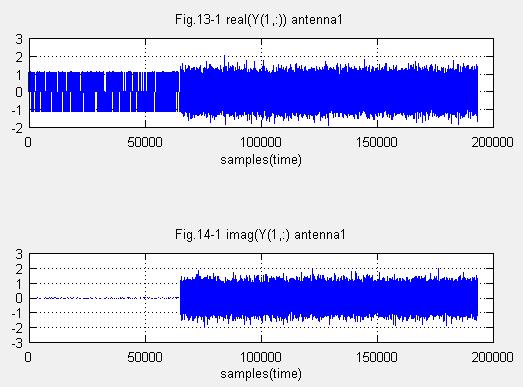
Fig.13-1,14-1はY=V_R'*X;%受信信号出力(実部と虚部)です。受信信号Xに受信重みV_Rを掛けてます。
これで特異値分解によるMIMO分離が出来ているようです。
コンステレーションを見てみます。FFTしてコンステレーションを描きます。
scatterplot(FFTout1(1,512:1511),1,0,'b.');シンボルは512〜1511に有ります。
振幅が大きくなってます、振幅補正が出来てない為です。後で振幅補正します。
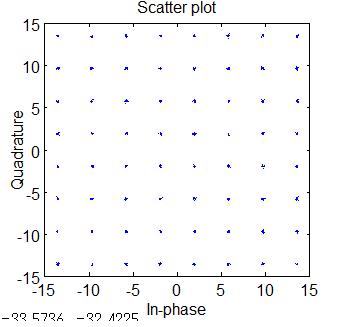
(6)受信信号行列Yを求める アンテナ2
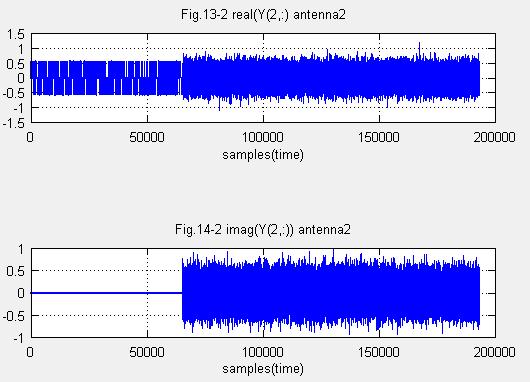
(7)OFDMのためのチャネル推定を行う アンテナ1、アンテナ2
チャネル推定後、位相とゲインの補正が必要です。
%受信機 チャネル推定 MIMOの場合
chEstSeq_rx1=FFTout1(:,1:seqLength);
phaseEst1=chEstSeq_rx1*mseq;
phaseEst12=phaseEst1;
phaseEst1=phaseEst1./abs(phaseEst1);%チャネル推定値
%比較のためもとの振幅1、位相遅れ無を確認する
phaseOrg1=chEstSeq1*mseq;
phaseOrg2=chEstSeq2*mseq;
%受信シンボルの位相補償とQAMの復調 振幅も補償する
%antenna1
phaseCompMat1=phaseEst1*ones(1,NofdmSymbol); %位相補償の値
rxSymbol12=FFTout1(:,(seqLength+1:end)).*conj(phaseCompMat1);
phaseEst13=phaseEst12./phaseOrg1;
gainCompMat1=phaseEst13*ones(1,NofdmSymbol); %振幅補償の値
rxSymbol13=rxSymbol12./abs(gainCompMat1);ここで振幅補償している。
rxSymbol1=round(rxSymbol13);
rxData1=qamdemod(MYvec(rxSymbol1),M);
Fig15-1は位相補償の図です、位相遅れはないようです。振幅は1で正規化しています。
Fig15-2は振幅補償の図です。振幅は2倍近くになっていて、位相遅れがないことがわかります。
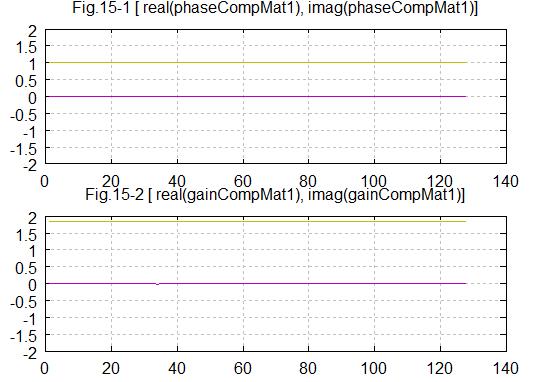
振幅補正後のコンステレーションを描いてみます。予定道理の64QAMコンステレーションです。
scatterplot(rxSymbol13(1,:),1,0,'b.');
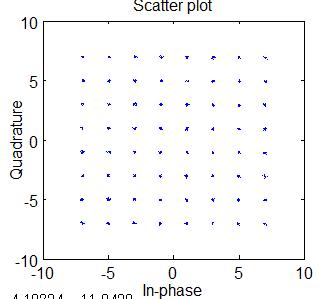
(8)受信シンボル アンテナ1
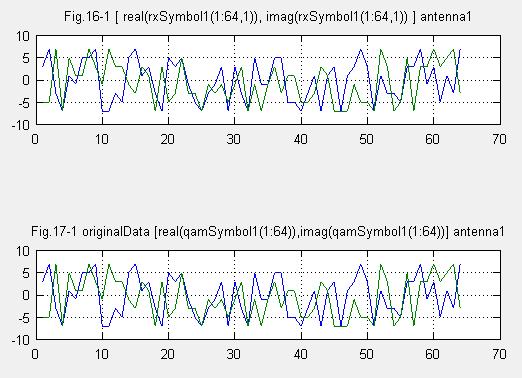
(9)受信シンボル アンテナ2
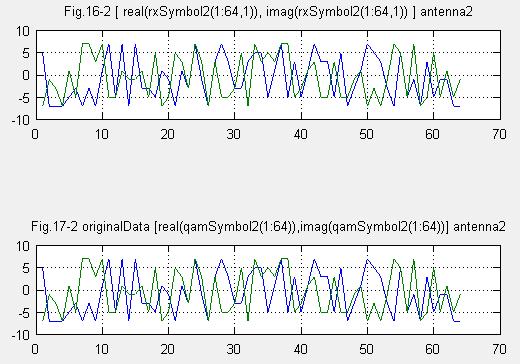
(10)受信(復調後)データ、送信元データ比較 アンテナ1
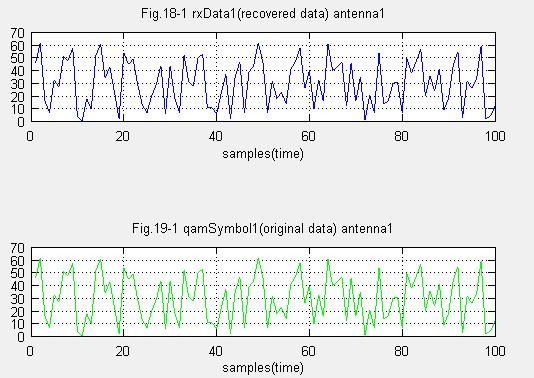
(11)受信(復調後)データ、送信元データ比較 アンテナ2
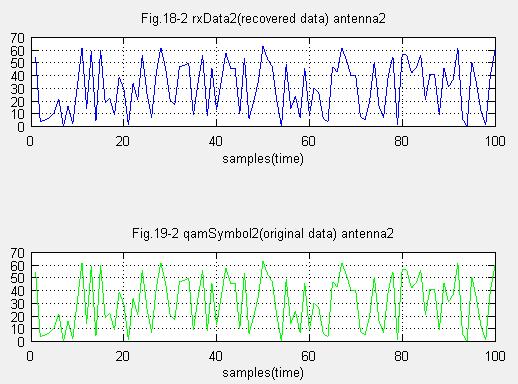
3、OFDM-64QAM信号 フェージングありの場合を確認してみます
遅延、フェージングを考慮し、GIを含めて計算してみます。
チャンネル推定様にM系列を先頭に付加します。OFDMの項で確認した内容と同じです。SN50dBを設定。
N_R=2;%受信アンテナ数
N_T=2;%送信アンテナ数
Nsub=128;% サブキャリア数
NofdmSymbol=1000;%OFDMシンボル数
Ns=Nsub*NofdmSymbol; %データシンボル数
N_GI=16; %GIの長さ
%フェージング設定
delay=[0;5];% 遅延τの設定
Tau1=30;
Mitigation_db=-10;
channelResponse1=MYdelayProfile(delay,Tau1,Mitigation_db);
channelResponse2=channelResponse1;
(1)M系列を含んだ信号系列を作る。GIも付加します アンテナ1
%送信機;データ信号生成 OFDM 64QAM
M=64;
data1=round(rand(Ns,1)*(M-1));%antenna1
qamSymbol1=qammod(data1,M);
data2=round(rand(Ns,1)*(M-1));%antenna2
qamSymbol2=qammod(data2,M);
SPCout1=reshape(qamSymbol1,Nsub,NofdmSymbol);% S/P変換 パラレルに変換 antenna1
SPCout2=reshape(qamSymbol2,Nsub,NofdmSymbol);% S/P変換 パラレルに変換 antenna2
%送信機 チャネル推定用系列
mseq=MYmseq([0;0;0;1;0;0;0;0;1]); % M系列の発生
seqLength=length(mseq); %チャネル推定系列長
chEstSeq1=ones(Nsub,1)*mseq.';%antenna1
chEstSeq2=chEstSeq1;%antenna2は1に同じ
%送信機 IFFT (GI付加)
IFFTout1=ifft([chEstSeq1,SPCout1]);%アンテナ1
GI1=IFFTout1((end-N_GI+1):end,:);
IFFTout2=ifft([chEstSeq2,SPCout2]);%アンテナ2
GI2=IFFTout2((end-N_GI+1):end,:);
sOFDM1=MYvec([GI1;IFFTout1]);
sOFDM2=MYvec([GI2;IFFTout2]);
sOFDM =[sOFDM1,sOFDM2];%antenna1と2を束ねる
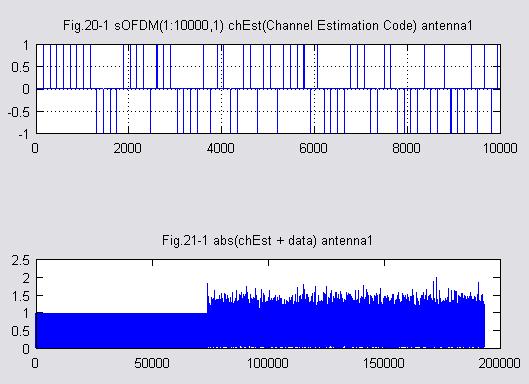
Fig.20-1は信号の先頭につけた”チャネル推定用系列”のM系列信号です。
Fig.21-1は変調信号全体ですが、65408サンプルまではチャネル推定用系列のM系列が付加されています(長さは511×128=65408)、それ以降はデータです。正確なデータ長は128×1000=128000とGI長128×16=2048ですので 全体で193408+2048=195456です。
(2)M系列を含んだ信号系列を作る。GIも付加します アンテナ2
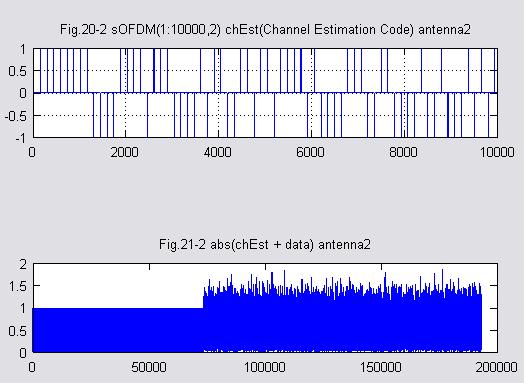
(3)送信信号系列Uを作る アンテナ1と2
周波数選択性フェージングを考慮してみます。アンテナ1,2とも同じフェージング特性としています。
H=MYcompNoise([N_R,N_T],1);%チャネル応答ベクトル 平均電力1の複素正規乱数
[V_R,LambdaM,V_T]=svd(H);%特異値分解
U=V_T*sOFDM.';
U1=U(1,:);
U2=U(2,:);
UU1=MYfSelFading(U1,delay,channelResponse1);
UU2=MYfSelFading(U2,delay,channelResponse2);
UU=[UU1.';UU2.'];
SNRdB=50;%
Pn=10^(-SNRdB/10);
X=H*UU+MYcompNoise(size(UU),Pn);%アンテナ入力信号
Y=V_R'*X;%受信信号出力
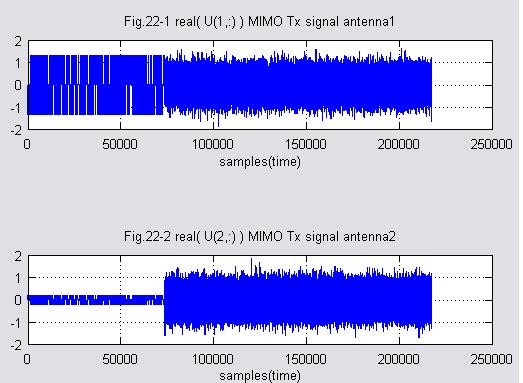
Fig.22-1,22-2は送信信号系列はU=V_T*Sですが、アンテナ1とアンテナ2ではM系列に相当する部分の振幅が異なっています。特異値分解されたV_Tの性質なんでしょうか。?これは特徴のようです。
(4)MIMO受信信号Xを求める アンテナ1と2
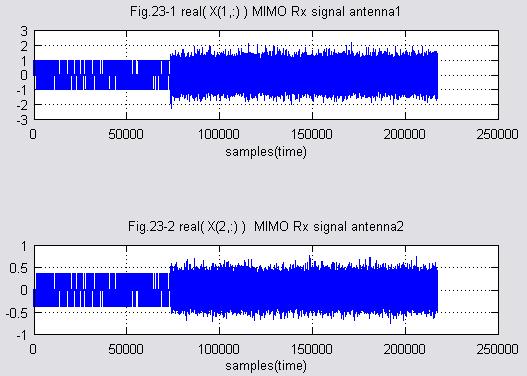
Fig.23-1, 23-2はMIMO受信信号X=H*V_T*S+複素ガウスノイズです。
(5)受信信号行列Yを求める アンテナ1
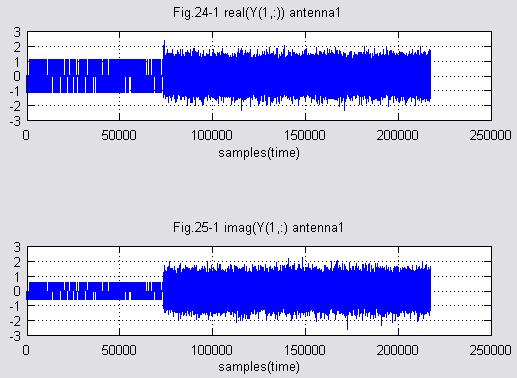
(6)受信信号行列Yを求める アンテナ2
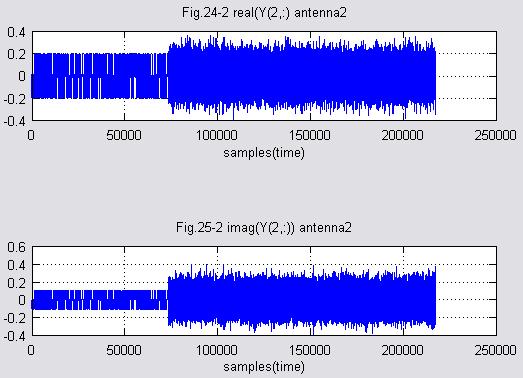
(7)OFDMのためのチャネル推定を行う アンテナ1、アンテナ2
%ここは OFDM受信機
%rxSPCOut1=reshape(Y(1,:),Nsub,NofdmSymbol+seqLength); %S/P
rxSPCOut1=reshape(Y(1,:),Nsub+N_GI,NofdmSymbol+seqLength); %S/P
rxSPCOut1(1:N_GI,:)=[];%GI除去
FFTout1=fft(rxSPCOut1);
%rxSPCOut2=reshape(Y(2,:),Nsub,NofdmSymbol+seqLength); %S/P
rxSPCOut2=reshape(Y(2,:),Nsub+N_GI,NofdmSymbol+seqLength); %S/P
rxSPCOut2(1:N_GI,:)=[];%GI除去
FFTout2=fft(rxSPCOut2);
%受信機 チャネル推定 MIMOの場合
chEstSeq_rx1=FFTout1(:,1:seqLength);
phaseEst1=chEstSeq_rx1*mseq;
phaseEst12=phaseEst1;
phaseEst1=phaseEst1./abs(phaseEst1);%チャネル推定値
chEstSeq_rx2=FFTout2(:,1:seqLength);
phaseEst2=chEstSeq_rx2*mseq;
phaseEst22=phaseEst2;
phaseEst2=phaseEst2./abs(phaseEst2);%チャネル推定値
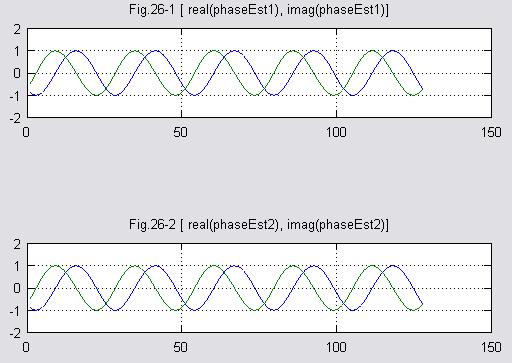
振幅、および位相の変化が発生しています。
(8)受信シンボル アンテナ1
%受信シンボルの位相補償とQAMの復調 振幅も補償する
%antenna1
phaseCompMat1=phaseEst1*ones(1,NofdmSymbol); %位相補償
rxSymbol12=FFTout1(:,(seqLength+1:end)).*conj(phaseCompMat1);
phaseEst13=phaseEst12./phaseOrg1;
gainCompMat1=phaseEst13*ones(1,NofdmSymbol); %振幅補償
rxSymbol13=rxSymbol12./abs(gainCompMat1);
rxSymbol1=round(rxSymbol13);
rxData1=qamdemod(MYvec(rxSymbol1),M);
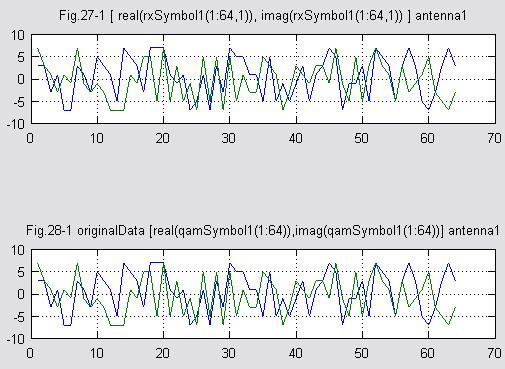
(9)受信シンボル アンテナ2
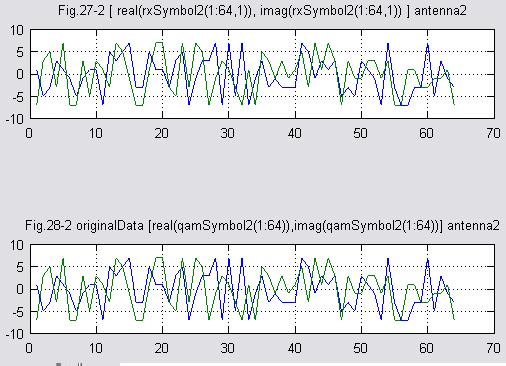
(10)受信(復調後)データ、送信元データ比較 アンテナ1
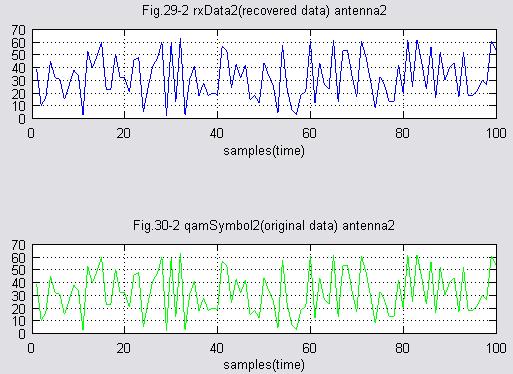
うまく受信されている様子です。
(11)受信(復調後)データ、送信元データ比較 アンテナ2
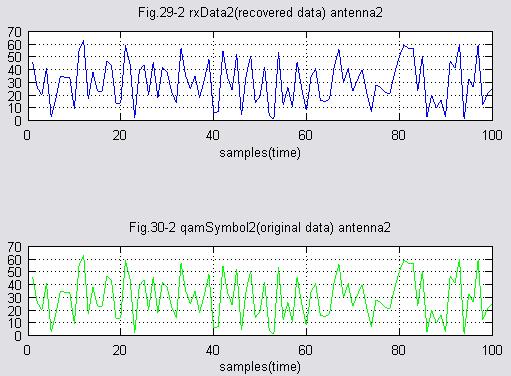
MIMO(2×2), ZF法による
Zero ForcingによるMIMOを考えます。チャネル応答にその逆システム(逆行列)を掛けてチャネル応答を打ち消す方法は、ノイズ増幅の問題はあるものの、もっとも手っ取り早いMIMOの手法です。
X=H*U+雑音
X=MIMOの受信信号
H=チャネル応答行列
U=送信信号行列
1、ZF法の例です
テキスト プログラム【例18】をZF法に改造して確認します。SNは20dBで計算。
もともと特異値分解で計算したところをZFにするのですから、送信重みはなし、受信重みはinv(H)とすれば確認できそうです。
アンテナ N_R=2,N_T=2の 2×2MIMO, Ndata=1000,BPSKデータです。
(1)信号系列を作る。ランダムなBPSK信号です。
%MY関数は参考文献(1)で紹介されている自作関数です
data=reshape(MYrandData(Ndata*N_T),N_T,Ndata);
U=bpskSymbols=MYbpskMod(data);%
H=MYcompNoise([N_R,N_T],1)%チャネル応答行列
(2)送信信号系列は送信重みが無いので、信号系列をそのまま送信します。U
SNRdB=10;%通信路SN
Pn=10^(-SNRdB/10);%
(3)MIMO受信信号
X=H*U+MYcompNoise([N_R,Ndata],Pn);%チャネル応答を掛ける,複素ガウスノイズを加える
(4)受信信号系列Yを求める
Y=inv(H)*X;
(5)受信信号系列を復調する。
recoverdata=MYbpskDemod(Y);
とSVDに比べ簡単になります。
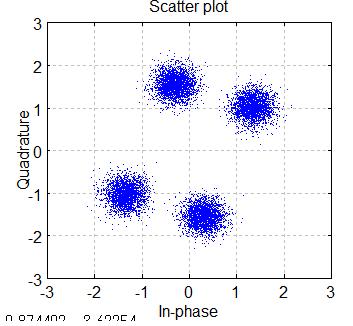
ここで、MIMO受信信号X(3)のコンステレーションを見てみます。
チャネル特性とノイズ特性が加わってます。
scatterplot(X(1,:),1,0,'b.')
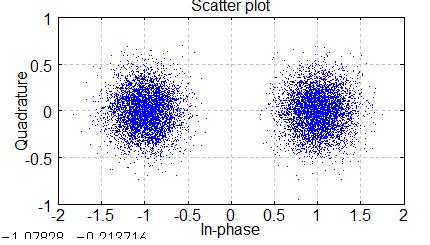
次にZF法でMIMO受信信号を分離した受信信号系列Y(4)のコンステレーションを見てみます。
分離されている様子です。ノイズは残ってます。
scatterplot(Y(1,:),1,0,'b.')
ZF法によるMIMO(2×2),OFDM-64QAM信号
Zero ForcingによるMIMOを考えます。チャネル応答にその逆システム(逆行列)を掛けてチャネル応答を打ち消す方法は、ノイズ増幅の問題はあるものの、もっとも手っ取り早いMIMOの手法です。
X=H*U+雑音
X=MIMOの受信信号
H=チャネル応答行列
U=送信信号行列
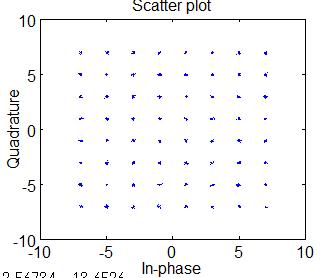
MIMO分離をしない(何もしない)状態のコンステレーション
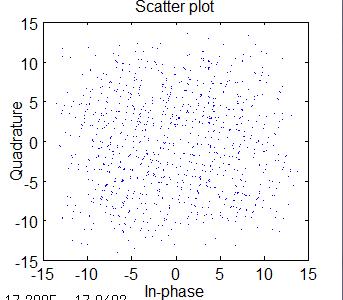
ZFの場合のコンステレーションです。ZFでも分離できています。
送信重みなし、フェージング無しですので振幅の変化はありません。
MMSEチャネル等化
MMSEチャネル等価(イコライザー)の式は参考文献(10)によれば
MMSEウェイト W = H H{ HHH+NI }-1 --- MMSEイコライザーの式
N:ノイズ、I:単位行列、Hは共役複素転置を表わす。
ここで受信信号ベクトルに、MMSEイコライザーの式のMMSEのウェイトWを乗算することで、他の送信アンテナからの干渉信号を抑圧することが出来る・・・・と記述されています。(この式でMIMO分離できるということのようです)
MIMO-OFDMの課題を考える
実用化されているMIMO技術ですが、どのような課題が残っているのでしょうか。気になるところですが、多くの論文等、サイト等があります。マルチユーザーMIMOや基地局連携MIMO等を考慮すると、初心者には敷居がかなり高くなりそうです。
実用に当たっては次の機会に学習したいと思います。
SC-FDMA
SC-FDMA(Single-Carrier Frequency Division Multiple Access)はLTEのUplinkに使われていますので学習してみます。
送信側信号(変調)の流れは
data ⇒ IQdataを時間領域に並べる ⇒ MポイントFFT(DFT) ⇒ サブキャリアにmapping ⇒ NポイントIFFT(時間領域)
・MポイントFFT(DFT)はMサブキャリア上にMシンボルを「拡散」する意味がある。
・最初のM-point FFTと大きなN-point IFFTで時間領域に戻っているので、時間領域での単一キャリア信号になる。
・PAPRは最初のIQdataを時間軸に並べたときに決まり、OFDMよりも低減される。
・サブキャリアにmappingしているので周波数帯域は任意に設定できるが、
選択するサブキャリアは隣接しているか(Localized mapping)、均一に配置する( distributed mapping(Interleaved Mapping))。
上記ではMポイントFFT、NポイントIFFT(MはNより小)となっているが、文献によってはM=Nで説明している場合がある。
M=Nの場合は計算上は問題ない特殊な場合と考えられる。実際にはInterleaved Mappingやサブキャリアの両端を0で埋める(Zeroing)操作などが実施されるためMはNより小さくなるのだろう。
とりあえずシミュレーションしてみます。先のOFDMの計算をベースにSCFDMの計算を追加します。
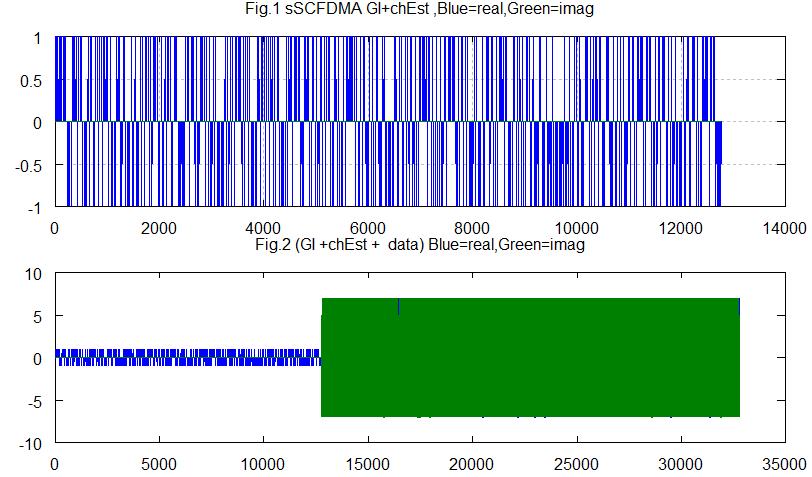
(1)送信機:送信データ(64QAM)をFFT変換し、チャネル推定信号を付加し、IFFT、GIを付加して送信信号を作る。
Fig.1はチャネル推定信号、Fig.2は送信全データです。
Nsub=20;% サブキャリア数(行に割り当て)
NofdmSymbol=1000;%変調シンボル数(列に割り当て)
Ns=Nsub*NofdmSymbol; %64QAMシンボル数
N_GI=5;% GI(gard interval) length
%送信機;データ信号生成 64QAM
M=64;
data=round(rand(Ns,1)*(M-1));
qamSymbol=qammod(data,M);
SPCout=reshape(qamSymbol,Nsub,NofdmSymbol);% S/P変換
y=fft(SPCout);%SPCoutが配列なので列方向にfftする
%送信機 チャネル推定用系列
mseq=MYmseq([0;0;0;1;0;0;0;0;1]); % M系列の発生
seqLength=length(mseq); %チャネル推定系列長 511
chEstSeq=ones(Nsub,1)*mseq.';
%送信機 IFFTおよびGIの付加
IFFTout=ifft([chEstSeq,y]); %チャネル推定は先頭の列に付ける
GI=IFFTout((end-N_GI+1):end,:);
sSCFDMA=MYvec([GI;IFFTout]);%GIを先頭の行に付ける
figure(1)
subplot(2,1,1)
plot([real(sSCFDMA(1:(N_GI+Nsub)*511)),imag(sSCFDMA(1:(N_GI+Nsub)*511))])
grid 'on'
title('Fig.1 sSCFDMA GI+chEst ,Blue=real,Green=imag') %chEst部のGIも含む
subplot(2,1,2)
plot([real(sSCFDMA(1:(Nsub*(NofdmSymbol+511)+N_GI*511))),imag(sSCFDMA(1:(Nsub*(NofdmSymbol+511)+N_GI*511)))])
title('Fig.2 (GI +chEst + data) Blue=real,Green=imag')
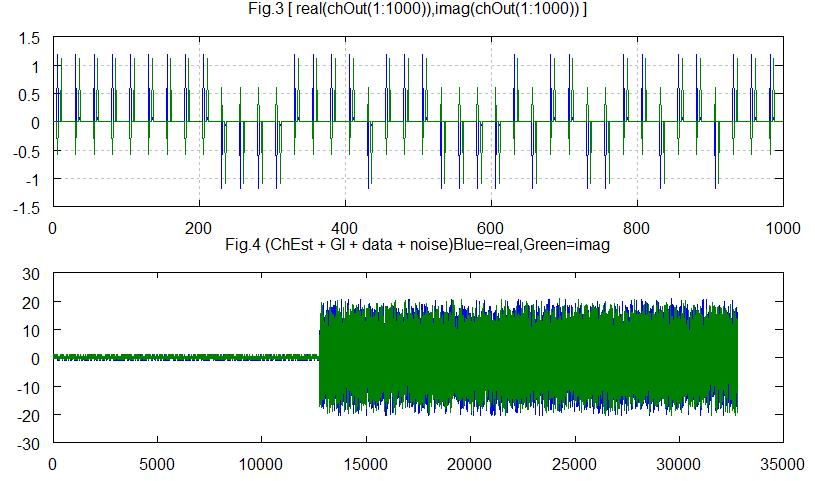
(2)周波数選択性フェージング通信路を考える。
Fig.3,Fig.4は周波数選択制フェージング通信路を考慮したものです。
%フェージング設定
delay=[0;5];% 遅延τの設定
Tau1=30;
Mitigation_db=-10;
channelResponse=MYdelayProfile(delay,Tau1,Mitigation_db);
%周波数選択制フェージング通信路
chOut=MYfSelFading(sSCFDMA,delay,channelResponse);
SNRdb=100; %SNRの設定
Pn=10^(-SNRdb/10)/Nsub;
chOut=chOut+MYcompNoise(size(sSCFDMA),Pn);%雑音の付加
figure(2)
subplot(2,1,1)
plot([real(chOut(1:1000)),imag(chOut(1:1000))])
grid 'on'
title('Fig.3 [ real(chOut(1:1000)),imag(chOut(1:1000)) ]')
subplot(2,1,2)
plot([real(chOut(1:(Nsub*(NofdmSymbol+511)+N_GI*511))),imag(chOut(1:(Nsub*(NofdmSymbol+511)+N_GI*511)))])
title('Fig.4 (ChEst + GI + data + noise)Blue=real,Green=imag')
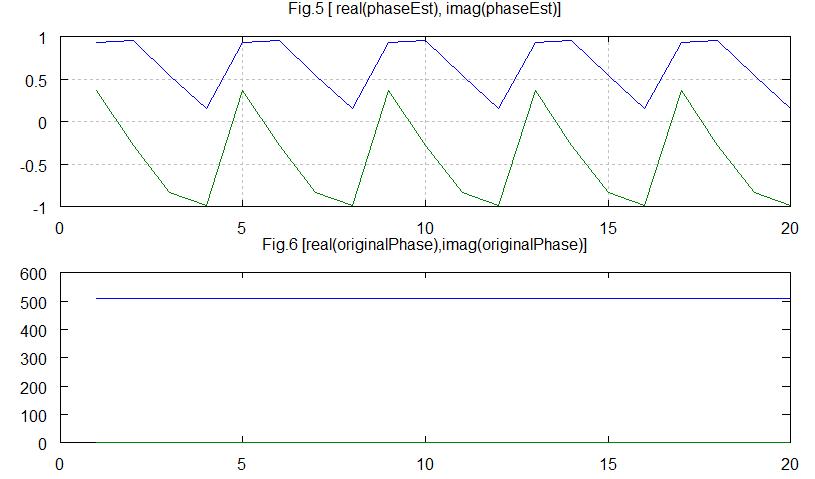
(3)受信機:チャネル推定を行う。
Fig.5,Fig.6はチャネル特性を表わしています。
Fig.5は今回使用した伝送路のチャネル特性
Fig.6は伝送路特性を無視した場合、チャネル推定の特性を比較のため表わしました。位相回転はなく、振幅は一定(511)です。511というのはチャネル推定系列長になっているようです。
%受信機
rxSPCOut=reshape(chOut,Nsub+N_GI,NofdmSymbol+seqLength); %S/P
rxSPCOut(1:N_GI,:)=[];%GI除去
FFTout=fft(rxSPCOut);
%受信機 チャネル推定
chEstSeq_rx=FFTout(:,1:seqLength);
phaseEst=chEstSeq_rx*mseq;
phaseEst2=phaseEst;
phaseEst=phaseEst./abs(phaseEst);%チャネル推定値
%比較のためもとの振幅1、位相遅れ無を確認する
phaseOrg=chEstSeq*mseq;
%phaseOrg=phaseOrg./abs(phaseOrg);%チャネル推定値
subplot(2,1,2)
plot([real(phaseOrg),imag(phaseOrg)])
%ylim([-2 2])
title('Fig.6 [real(originalPhase),imag(originalPhase)]')
(4)受信シンボルの位相補償とQAMの復調 振幅も補償する
Fig.7は復調したデータ(数20)。
Fig.8は送信元データです、Fig.7と一致しているようなので、無事復調されているようです。
%受信シンボルの位相補償とQAMの復調 振幅も補償する
phaseCompMat=phaseEst*ones(1,NofdmSymbol); %位相補償
rxSymbol2=FFTout(:,(seqLength+1:end)).*conj(phaseCompMat);
phaseEst3=phaseEst2./phaseOrg;
gainCompMat=phaseEst3*ones(1,NofdmSymbol); %振幅補償
rxSymbol3=rxSymbol2./abs(gainCompMat);
rxSymbol=round(rxSymbol3);
rxData=qamdemod(MYvec(rxSymbol),M);
rxDataIFFT=ifft(rxData);
rxSymbolIFFT=ifft(rxSymbol);
Appendix
疑似逆マトリクスの性質
・MMSE IRCの式で下記が使われている
A+: マトリクスAの疑似逆マトリクス
A+ = (AHA)+AH = AH (AAH)+
ということなので、MMSE IRCの式が次のように書ける
MMSEウェイト
W = H H{ HHH+NI }-1
= { HHH+NI }-1H H
参考文献(10)では右の式が、参考文献(11)では左の式を使っていました。
参考文献
(1)「MATLABによるディジタル無線通信技術」神谷 幸宏、2008年、コロナ社
(2)MIMO無線通信における伝搬路推定のモデリングに関する研究
(3)マルチパス環境におけるビームフォーマ法を用いた波数及び到来方向の推定に関する研究
(4)MATLAB Communications Toolbox User'guide
(5)マルチパス通信路
(6)通信システム
(7)川口英「Excelを使ったOFDMシミュレーション」トランジスタ技術2008.11月号 pp153-157
(8)「アダプティブアンテナ技術」菊池 信良、平成15年10月10日 オーム社
(9)Albert Serra Pages "A Long Term Evolution Link Level Simulator"
(10)NTTDocomoテクニカルジャーナルVol.14 NO.1 PP66-75
(11)MIMO with MMSE equalizer




































































