clear
t=0:0.001:1.3; # サンプリング周波数1000Hz
y=sin(2*pi*50*1000/512*t)+sin(2*pi*100*1000/512*t); #50*1000/512Hzと100*1000/512Hzの信号
Y=fft(y,512); #512フーリエ変換により周波数領域に変換
Pyy=Y.*conj(Y)/512; # Pyy-スペクトル密度conj-複素共役
f=1000*(0:511)/512;
subplot(2,1,1)
plot(f,Pyy(1:512))
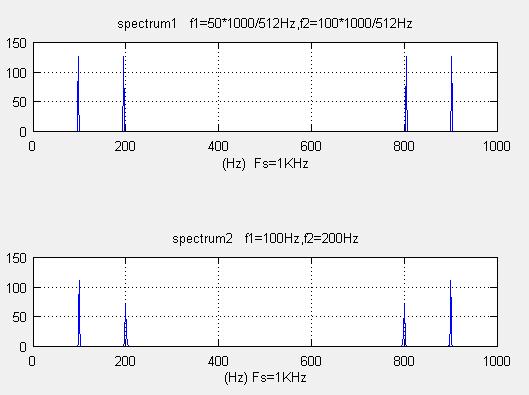
title("spectrum1 f1=50*1000/512Hz,f2=100*1000/512Hz")
xlabel("(Hz)")
grid "on";
y=sin(2*pi*100*t)+sin(2*pi*200*t); #100Hzと200Hzの信号
Y=fft(y,512); #512フーリエ変換により周波数領域に変換
Pyy=Y.*conj(Y)/512; # Pyy-スペクトル密度conj-複素共役
f=1000*(0:511)/512;
subplot(2,1,2)
plot(f,Pyy(1:512))
title("spectrum2 f1=100Hz,f2=200Hz")
xlabel("(Hz)")
grid "on";

他に注意したいことは、振幅スペクトラムが正しく再現できる周波数とできない最小分解周波数があるようです。Δf最小分解周波数=FFTのサンプリング周波数/FFT点数の整数倍であれば、振幅スペクトラムは再現できます。
例題のspectrum1は50*1000/512Hzと100*1000/512Hzの信号のFFT、spectrum2は100Hzと200Hzの信号のFFTである。振幅スペクトラムが同じくならないで、100Hz,200Hzのは小さくなっているので注意が必要です。
・2008年5月15日(書き始め)
パスバンド複素化( 直交復調 )
入力信号ーー>*(掛ける)cosーー> I成分
入力信号ーー>*(掛ける)sinーー> Q成分
上記の様にsinを乗算すれば正の信号が、-sinを乗算すれば負の信号が取り出せる。このようiなデジタルミキサでは一つの信号が取り出せる。
ヒルベルト変換
hilbert(x),hilbert(x,n)関数が用意されてます。
clear
% FFTポイント数512
Y=zeros(512,1);%512ポイント全クリア
Y(150)=0-256*i;%150番目にスペクトラムを立てる
Y(413)=0-256*i;%413番目にスペクトラムを立てる
Y(463)=0-256*i;%463番目にスペクトラムを立てる
Pyy=Y.*conj(Y)/512; # Pyy-スペクトル密度conj-複素共役
subplot(2,1,1)
plot(Pyy)
axis([0 512 0 150])
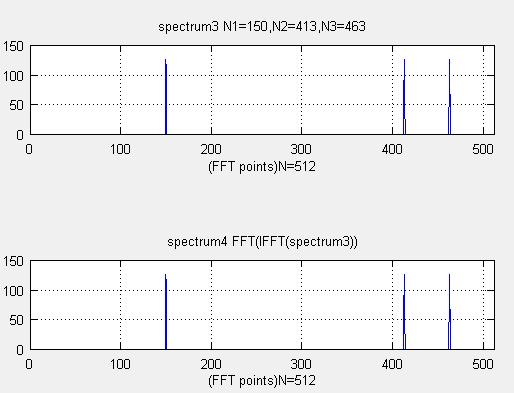
title("spectrum3 N=150,413,463")
xlabel("(FFT points)")
grid "on";
IY=ifft(Y); %IFFT
FY=fft(IY); %FFT
Fyy=FY.*conj(FY)/512; # Pyy-スペクトル密度conj-複素共役
subplot(2,1,2)
plot(Fyy)
axis([0 512 0 150])
title("spectrum4 FFT(IFFT(spectrum3))");
xlabel("(FFT points)")
grid "on";
clear
t=0:0.001:1.3;# サンプリング周波数1000Hz
y=sin(2*pi*50*1000/512*t)+sin(2*pi*100*1000/512*t); #50*1000/512Hzと100*1000/512Hzの信号
Y=fft(y,512); #512フーリエ変換
Pyy=Y.*conj(Y)/512; # Pyy-スペクトル密度conj-複素共役
subplot(2,1,1);
plot(t,y);
axis([0 0.05 -2 2])
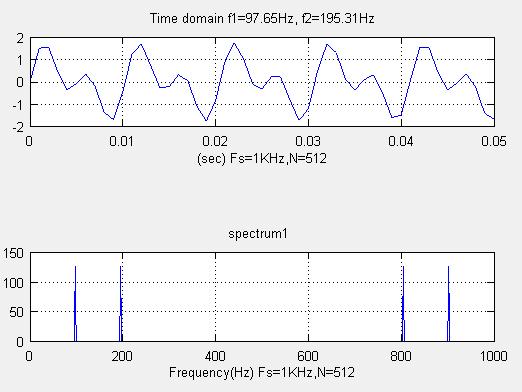
title("Time domain f1=97.65Hz, f2=195.31Hz")
xlabel("(sec)")
grid "on";
f=1000*(0:511)/512;
subplot(2,1,2)
plot(f,Pyy(1:512))
title("spectrum1 ")
xlabel("(Hz)")
grid "on";
nn = 512;
ze = zeros(2*nn,1);
for m=1:nn
ze(2*(m-1)+1)=y(m);
ze(2*(m-1)+2)=0; %0挿入
end
figure
tt=0:0.0005:0.5115;
subplot(2,1,1)
plot(tt,ze)
axis([0 0.05 -2 2])
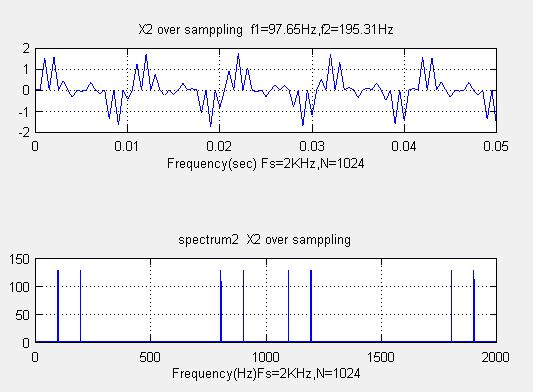
title("X2 over samppling f1=97.65Hz,f2=195.31Hz")
xlabel("(sec)")
grid "on";
FFTze=fft(ze,1024);
PPyy=FFTze.*conj(FFTze)/512; # Pyy-スペクトル密度conj-複素共役
subplot(2,1,2)
f2=2000*(0:1023)/1024;
plot(f2,PPyy(1:1024));
title("spectrum2 X2 over samppling ")
xlabel("(Hz)")
grid "on";
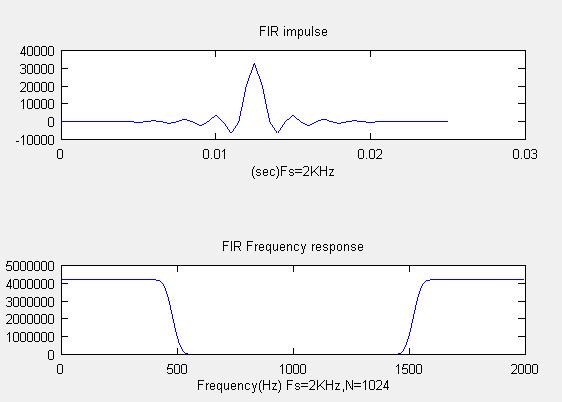
%FIR フィルター
F=[8;0;24;0;58;0;-120;0;221;0;-380;0;619;0;-971;0;1490;0;-2288;0;3649;0;-6628;0;20750;32768;20750;0;-6628;0;3649;0;-2288;0;1490;0;-971;0;619;0;-380;0;221;0;-120;0;58;0;-24;0;8];
figure
subplot(2,1,1)
tt2=0:0.0005:0.025;
plot(tt2,F);% impulse responseはフィルターそのもの
xlabel("(sec)")
title("FIR impulse")
yF=fft(F,1024);%FIRフィルターのFFT
yFyy=yF.*conj(yF)/1024; # Pyy-スペクトル密度conj-複素共役
f2=2000*(0:1023)/1024;
subplot(2,1,2)
f2=2000*(0:1023)/1024;
plot(f2,yFyy(1:1024));
xlabel("(Hz)")
title("FIR Frequency response");
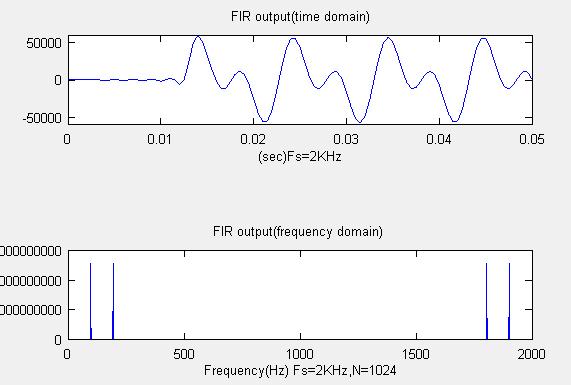
fout=conv(ze,F); %zeはオーバーサンプリング2倍した前述のデータ FはFIRフィルター
figure
subplot(2,1,1)
tt3=0:0.0005:0.5365;
plot(tt3,fout)
axis([0 0.05 -60000 60000]);
xlabel("(sec)")
title("FIR output(time domain)");
fyF=fft(fout,1024);
fyFyy=fyF.*conj(fyF)/10241; # Pyy-スペクトル密度conj-複素共役
subplot(2,1,2)
plot(f2,fyFyy(1:1024));
xlabel("(Hz)")
title("FIR output(frequency domain) ");

octaveに用意されているsinc関数があります。
戻り値にはpiが含まれていることに注意します。
File: sinc (x)
Return sin(pi*x)/(pi*x).
・もとのフィルタ係数を等間隔に取り出しフィルタ・バンクに展開した構造。
・フィルタの計算時間をサンプリング時間で均等に割り振ることが可能。
・消費電力削減、回路規模削減が可能になります。
詳しくは Blackfinさんに
Klabさんなどのサイト掲載されてました。
FIRフィルターをポリフェーズ分解(変換)することによってポリフェーズ・フィルタを作ることができます。
octaveで関連する関数が用意されています。
[y h]= resample(x,p,q), y = resample(x,p,q,h)
「Change the sample rate of x by a factor of p/q. This is performed using a polyphase algorithm. The impulse response h of the antialiasing filter is either specified or either designed with a Kaiser-windowed sinecard」
ノーブル恒等変換
ポリフェーズフィルタはポリフェーズ変換とノーブル恒等変換が組み合わせて使われています。ノーブル変換は下記の等価変換のことです。
アップサンプリングの場合を例にとると、アップサンプラの前にある信号処理段H(z)が、アップサンプラの後ろに移動された場合、その処理がH(zL )になります。
ダウンサンプリング
x(n)→ ↓M → H(z)→y1(n) ⇔ x(n)→ H(zM) → ↓M →y1(n) は等価
アップサンプリング
x(n)→ H(z) → ↑L → y2(n) ⇔ x(n)→ ↑L → H(zL ) →y2(n) は等価
ポリフェーズ分解
周波数の有効利用のため信号(シンボル)の帯域制限を行う必要がありますが、送信データの情報を失わないための帯域制限の条件(ナイキスト基準)、およびその条件を満足するフィルタ(ロールオフフィルタ)が重要になってきます。
(1) T秒ごとに標本化された標本をフィルタを通したとき,出力波形のT秒ごとの標本値が元の値と完全に等しくなるようなフィルタである。T(sec)毎の入力波形の情報は出力側で維持されているので、この状態を零符合間干渉(零ISI:零Inter-Symbol Interference)と呼ばれ、このフィルタがナイキストフィルタです。
(2) 単一キャリア変調信号の場合のサイドローブ制限などに使われてます。
(3) 理想フィルタは実現困難であるため、ナイキスト2乗余弦フィルタが良く用いていて、シンボル・クロック周波数のちょうど半分の周波数を境に、左右が奇対称の周波数特性を持つフィルタになる。
(4) しかしオーバーシュートやアンダーシュートが普通に発生し振幅特性が暴れる。
(5) 上記理由によりロールオフ・フィルタが必要になる。
Matlabを使えばコサインロールオフ・フィルタ設計ツール 関数rcosineが付いているようですので、Matlabに譲ったほうがよさそうです。
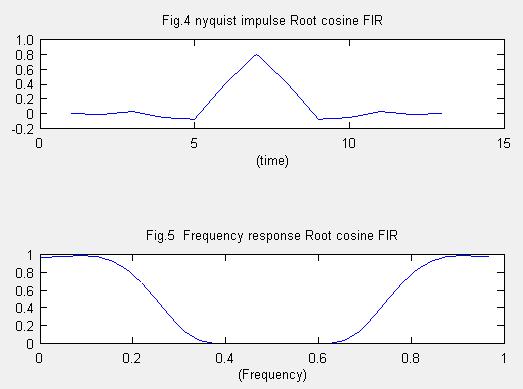
注意点ですが、octaveのsinc関数はsinc(x)=sin(pi*x)/(pi*x)です。piがあらかじめ入ってます。
Fig.1はsinc関数のインパルス応答、Fig.2はfs=0.25で作ったナイキストフィルタです。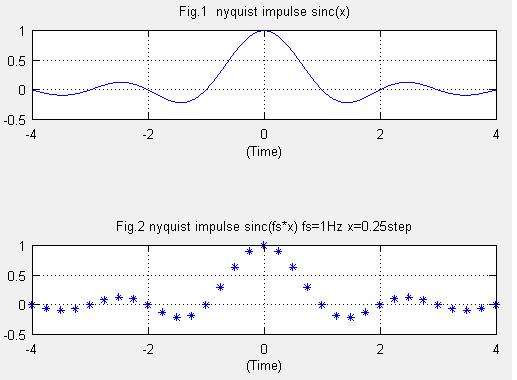
figure(1)
x=(-4:0.1:4);
y=sinc(x);
subplot(2,1,1), plot(x,y);
xlabel("(Time)")
title("Fig.1 nyquist impulse sinc(x)")
grid "on";
fs=1;%hz
x2=(-4:0.25:4);%msec
y2=sinc(fs*x2);
subplot(2,1,2), plot(x2,y2,"*");
xlabel("(Time)")
title("Fig.2 nyquist impulse sinc(fs*x) fs=1Hz x=0.25step")
grid "on";
figure(2);
FTP=128;
yf=fft(y2,FTP);
YF=yf.*conj(yf)/FTP; # Pyy-スペクトル密度conj-複素共役
f2=1*(0:FTP-1)/FTP;
subplot(2,1,1);
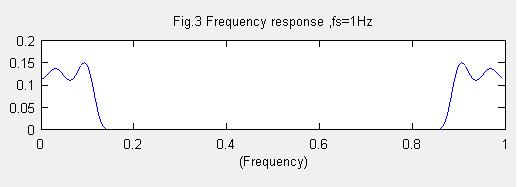
plot(f2,(YF));
xlabel("(time)")
title("Fig.3 Frequency response ,fs=1Hz")
xlabel("(Frequency)")
サンプリングレートが1であるディジタル信号の利用のために、サンプリングレート2のルートコサインFIRロールオフフィルタを設計します。
num = rcosine(1,2,'fir/sqrt')
num =
Columns 1 through 7
0.0021 -0.0106 0.0300 -0.0531 -0.0750 0.4092 0.8037
Columns 8 through 13
0.4092 -0.0750 -0.0531 0.0300 -0.0106 0.0021
ここで、ベクトルnumは、z-1のべきの昇順にフィルタの係数を含みます。
はどうなるでしょうか
FI=[ 0.0021 -0.0106 0.0300 -0.0531 -0.0750 0.4092 0.8037 0.4092 -0.0750 -0.0531 0.0300 -0.0106 0.0021];
実際にはフーリエ変換を2回も実行するのは処理が重たいので、フーリエ変換しない方法が提案されてます。
シミュレーションならばhilbert(x),hilbert(x,n)関数が便利です。 直交変調
I信号ーー>*(掛ける)cosーー>①
Q信号ーー>*(掛ける)sinーー>②
直交変調信号は①+② QPSK, QAMなど
直交復調
入力信号ーー>*(掛ける)cosーー>③ I成分
入力信号ーー>*(掛ける)sinーー>④ Q成分
直交関数について復習します。相互相関がゼロ、畳みこみがゼロということですが、フーリエ変換された信号はフーリエ級数 ejωt+ej2ωte+j3ωt+・・・式①で表されます。ここでcoskxとsinlx (k,l=1,2,3...)は[-π,π]で直交関係にあるということで式①の各々の項同士の畳みこみはゼロになるような気がします(実際にゼロになります、例えばejωtとej2ωtの畳みこみがゼロ)。従ってフーリエ変換は直交関数になります。
他の直交関数にDCT(コサイン変換)があります。フーリエ変換とは違って積分区間を2πからπに改め、cosだけで寄関数を表現している。関数はdct(x)があります。
パスバンド複素化( 直交復調 )
入力信号ーー>*(掛ける)cosーー> xi I成分
入力信号ーー>*(掛ける)sinーー> xq Q成分
(4)参考文献2のp97には複素ミキサの詳細が載ってます。それによりますと
入力 xi,xq 出力 y = yi+ i*yq
yi=cos(ωt)*xi-sin(ωt)*xq
yq=sin(ωt)*xi+cos(ωt)*xq
ここでωが負の場合は
yi=cos(ωt)*xi+sin(ωt)*xq
yq= -sin(ωt)*xi+cos(ωt)*xq
となります。
(4)実際にはsin,cos信号を作るために、NCO(数値制御発信器)が用いられている。
これをシミュレーションで確認してみます。以下に確認結果を示します。
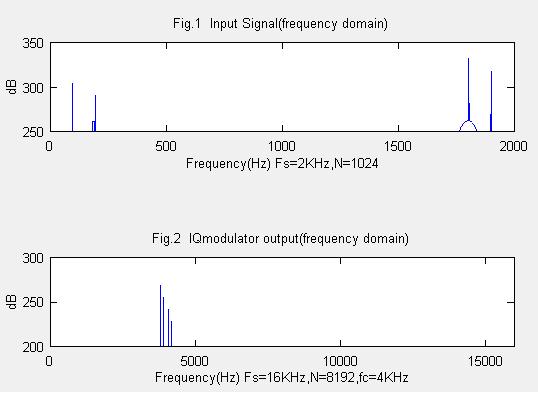
[入力信号] Fig1は入力信号スペクトラムとします。4本のスペクトラムがあります。レベルをわざと違うようにして、スペクトラムの区別ができるようにしておきます。中心より左側の2本のスペクトラムは正の周波数を表わし、右側の2本のスペクトラムは負の周波数を表しています。
[UP conversion 直交変調] Fig2はFig1の入力信号をIF(4KHz)で変調(UP conversion)したものです。IF(4KHz)より低いほうに負の周波数成分、高いほうに正の周波数成分のスペクトラムがIF付近に集まります。
[シミュレーションでの注意点]は、入力信号とIF信号のサンプリング周期を合わせることです。共に16KHzサンプリング周期になるように、入力信号をオーバーサンプリング(D/Aコンバータを想定し0次ホールドでオーバーサンプリング)して、16KHzサンプリンにし、いらないスペクトラムを除くためにFFTをかけスペクトラム上でオーバーサンプリングをデータを作りました。その信号を入力信号としています。
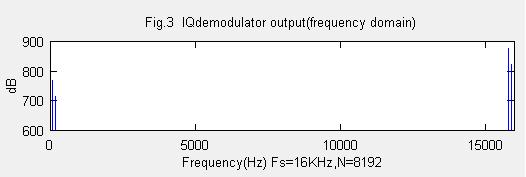
計算上の注意点は、Octaveでのzのべき乗の並べ方です。zのべき乗の降順に並べて計算するのが標準です。これに従いますと、SINCコムフィルタは
(zM-1)/(MzM-MzM-1)
M=8の場合を考えて、Octaveで伝達関数tfを計算し周波数特性を書いてみます。参考文献(2)90ページを参考にしてます。
sys=tf([1 0 0 0 0 0 0 0 -1],[8 -8 0 0 0 0 0 0 0],0.0000625)
fw=(0:10:(32000-1)*pi);%16kHz 2*1600=3200
[gain phase] = bode(sys, fw);
gain_db = 20*log10(gain);
subplot(2,1,1);
fss=(0.5/pi:5/pi:1600); % f=0.5/pi
plot(fss,gain_db);
title("Fig.4 SINC filter M=8");
ylabel("dB");
xlabel("Frequency(Hz)") ;
axis([1 16000 -70 0]);
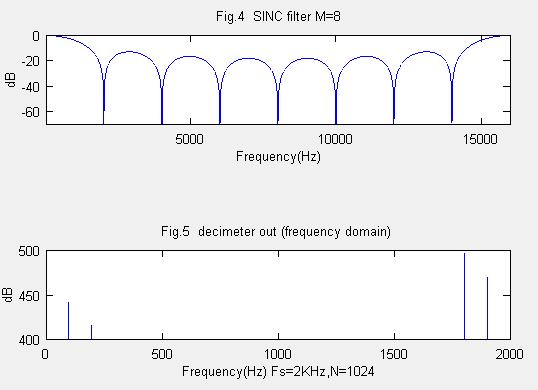
filter関数をつかっての計算方法は(MM=8)、
A=[MM -MM 0 0 0 0 0 0 0];
B=[1 0 0 0 0 0 0 0 -1];
y1=filter(B,A,y_i);
PN9の場合の例
init = [1 1 1 1 1 1 1 1 1]; % シフトレジスタの初期状態量
poly = [1 0 0 0 0 1 0 0 0 1]; % フィードバック回路(多項式)
number = 51; % PNシーケンス信号の長さ
out = pnsamp1(init,poly,number); % PNシーケンス信号作成
PN15の場合の例
init = [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]; % シフトレジスタの初期状態量
poly = [1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1]; % フィードバック回路(多項式) 0x6000
number = 32767; % PNシーケンス信号の長さ
out = pnsamp1(init,poly,number); % PNシーケンス信号作成
/// pnsamp1 //Matlab の例題 ///////////////
r=init;
g=poly;
br = zeros(1,length(r));
for t=1:number
br(1) = mod(r*[g(2:end)]',2);
br(2:end) = r(1:end-1);
out(t) = r(end);
r = br;
end
M=64;
x = [0:M-1];
y = qammod(x,M); %64QAM
%grey codeが指定できないので無理やりマッピングする。
ip = [0:7]; % decimal equivalent of a four bit binary word
opL = bitxor(ip,floor(ip/2)); % decimal equivalent of the equivalent four
opM = opL*sqrt(M);
hold on; % 注釈を同じ図に置く
scatterplot(y,1,0,'b.'); %
legend 64QAM;
%変調信号yにマッピングする配列opを作る
n=0;
for c=1:sqrt(M)
for l=1:sqrt(M)
n=n+1;
op(n)=opL(c)+opM(l);
endfor
endfor
% 点に番号を付ける
for jj=1:length(y)
text(real(y(jj))+0.15,imag(y(jj)),dec2bin(op(jj)));
endfor
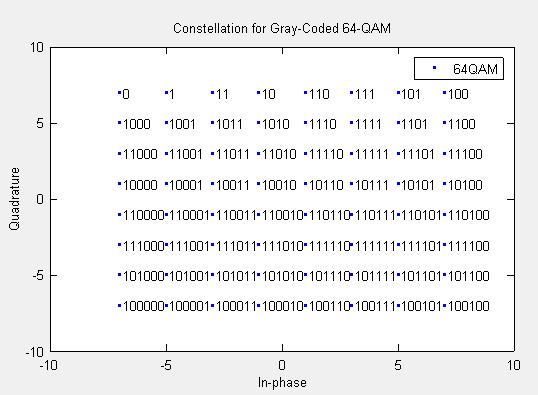
title('Constellation for Gray-Coded 64-QAM');
hold off;
OFDMの文献をよく見かけるようになりました。トラ技(参考文献3)にも連載記事が始まってますので、詳細はそちらに期待したいと思います。
なぜOFDMなのか?そのエッセンスが参考文献(4)に記されていました。2つあります。
(1)信号の低速化
周波数選択性フェージングはデータ伝送速度が低い信号には影響がない。
なるほど、OFDMはサブチャンネルに信号をのせて送りますが、そのサブチャンネルの伝送速度は低いのです。例えば、1000のサブチャンネルがあり、50Mbpsの伝送をする場合、1つのサブチャンネルは50/1000=50Kbpsでいいのです。
(2)信号の並列化
データの高速伝送を行うため、異なる周波数で同時に並行して伝送する。全体として高速伝送になります。
ということですが、そのためには直交変換関数(FFT)を使って処理していきます。
本サイトでも、PICマイコンを使ってOFDMのまねごとをしようとしています。使用したdsPICにはFFT/IFFT関数が用意されていますので使ってみました。またこちら(Octave_MIMO)ではもう少し踏み込んでいます。