・2008年3月13日（書き始め）
参考文献 （１）田澤 勇夫 「ペルチェを使った範囲±50℃，誤差0.01℃以内の恒温槽の製作（設計偏）」トランジスタ技術 2007年3月号
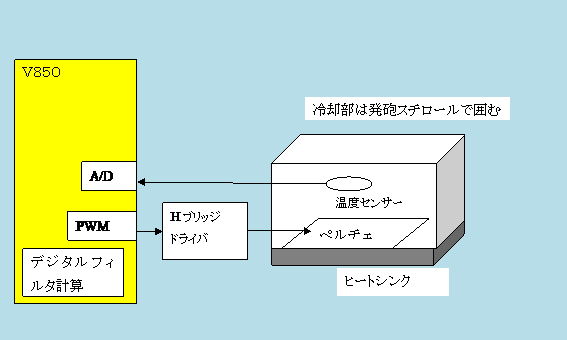
（１）温度センサーを１０Hｚでサンプリングする
・サーミスタの出力を25℃のときに１．５Vになるように回路設計します。すなわち今回の制御の目標値は２５℃として、サーミスタの出力を常に１．５Vになるように制御すればよいことになります。
・ペルチェの制御帯域を１Hz程度と想定し、A/Dのサンプリング周波数を１０Hｚ程度とします。１０Hｚのインターバル割り込みをTMP2で行います。A/Dデータのノイズを下げるため５ポイントの移動平均を取っています。
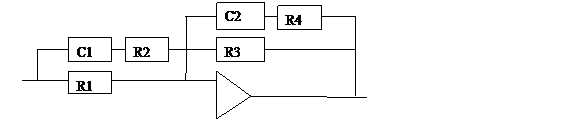
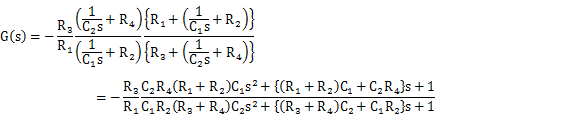
R1=18KΩ,R2=10KΩ,R3=10MΩ,R4=68KΩ,C1=118uF,C2=202.2uF（実験で求めた値）とすれば
Cs^2+Ds+E
H(s)=------------
s^2+As+B
A=0.84794
B=0.0004162
C=7.74731
D=1.40519
E=0.06121
数値計算ソフトウェアOctaveの関数を使って離散化伝達関数を求め、デジタルフィルタを作成します。
sys=tf([C,D,E],[1,A,B]);
hd=c2d(sys,"matched",0.1); %サンプリング時間を0.1秒とした。
Zer,Polが出力される。0次ホールドで離散化される。
zer 0.98919 0.99276
pol 0.91875 0.9995
K=7.4956
tsam=0.1
zp2tfを使って離散化伝達関数を求める
（zer、polは使用しないので、最初から離散化伝達関数を求められればいいのですが）
（＊）後でわかったことですが、 sys=tf([C,D,E],[1,A,B],tsam);とすれば離散伝達関数が求まります。
tsam=サンプリング時間。結果がちょっと異なりますので、注意？が必要です。
% [htn,htd]=zp2tf([0.98919,0.99276],[0.91875 ,0.9995],7.4956)
[htn,htd]=zp2tf(hd.zer,hd.pol,hd.k) %上の式と同じ結果になる
y(z) 7.4956 - 14.8559z^-1 + 7.3609z^-2
---- = ----------------------------------
u(z) 1 - 1.91825z^-1 + 0.91829z^-2
従って
y[n] = 1.91825y[n-1] - 0.91829y[n-2] + 7.4956u[n] - 14.8559u[n-1] + 7.3609u[n-2]
この式をV８５０に組み込んで見ます。
アナログ補償器のボード線図は下記のようになります。
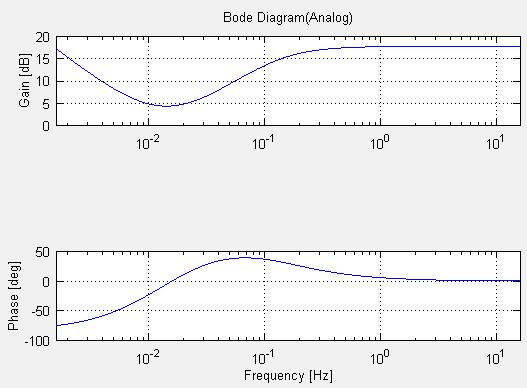アナログ補償器
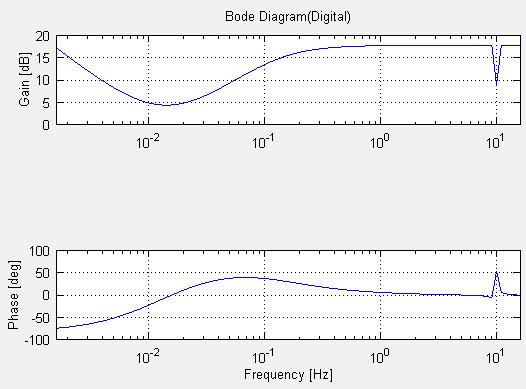デジタル補償器
計算プログラムは
%bodec.m
A=0.84794;
B=0.0004162;
C=7.74731;
D=1.40519;
E=0.06121;
アナログ補償器は
sys=tf2sys([C,D,E],[1,A,B]);
w = logspace(-2,2,100);
[mag,phase] = bode(sys,w);
sysout(sys);
figure(1);
subplot(2,1,1);
f = w/(2*pi); % rad/sec --> Hz
semilogx(f,20*log10(mag)); % ゲインの応答
title('Bode Diagram(Analog)');
ylabel('Gain [dB]');
grid on
set(gca,'XLim',[f(1) f(end)]); % 表示範囲の変更
subplot(2,1,2);
semilogx(f,phase); % 位相の応答
xlabel('Frequency [Hz]');
ylabel('Phase [deg]');
grid on
set(gca,'XLim',[f(1) f(end)]) % 表示範囲の変更
デジタル補償器は
hd=c2d(sys,"matched",0.1); %サンプリング時間を0.1秒とした。
[htn,htd]=zp2tf(hd.zer,hd.pol,hd.k);
w = logspace(-2,2,100);
[mag,phase] = bode(hd,w);
sysout(hd);
figure(2);
subplot(2,1,1);
f = w/(2*pi); % rad/sec --> Hz
semilogx(f,20*log10(mag)); % ゲインの応答
title('Bode Diagram(Digital)');
ylabel('Gain [dB]');
grid on
set(gca,'XLim',[f(1) f(end)]); % 表示範囲の変更
subplot(2,1,2);
semilogx(f,phase); % 位相の応答
xlabel('Frequency [Hz]');
ylabel('Phase [deg]');
grid on
set(gca,'XLim',[f(1) f(end)]) % 表示範囲の変更
(１）−１ Fig6-1に制御対象のステップ応答を示します。
%G(s)=c/{(s+a)(s+b)} %制御対象
a=0.2;
b=0.3;
c=1;
Ac=[0 1;-a*b -(a+b)];
Bc=[0; 1];
Cc=[1 0];
Dc=[0];
%ステップ応答を計算してみます（Fig6-1 オイラー法です）
%オイラー法
u=1;
dt = 0.05;
tf=50;
x=[0;0];
xx = [];
nn=0;
for t=0:dt:tf
nn = nn+1;
xx(:,nn)=x;
y(:,nn)=Cc*x;
dx = Ac*x + Bc*u;
x = x + dx*dt;
endfor
t=0:dt:tf;
%////////////// figure(6-1)////////////////////
figure();
grid on
subplot(2,1,1);
plot(t,xx)
title('Step response(Output x1=y,x2)')
xlabel('time(sec)')
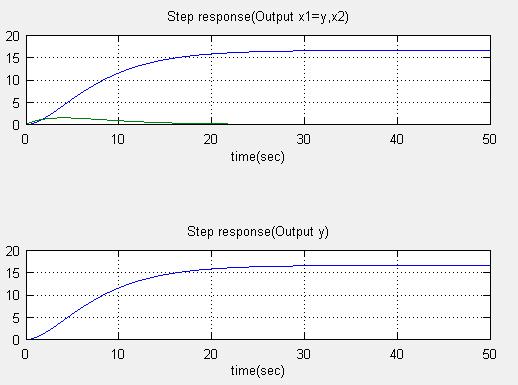Fig6-1ステップ応答
（１）−２ 制御対象のボード線図を書いてみます(Fig6-2)
sys2=tf2sys([c],[1 (a+b) a*b]);
w = logspace(-2,2,100);
[mag,phase]=bode(sys2,w);
sysout(sys2);
subplot(2,1,1)
f = w/(2*pi); % rad/sec --> Hz
semilogx(f,20*log10(mag)) % ゲインの応答
title('Bode Diagram (Object)')
ylabel('Gain [dB]')
grid on
set(gca,'XLim',[f(1) f(end)]) % 表示範囲の変更
subplot(2,1,2)
semilogx(f,phase) % 位相の応答
xlabel('Frequency [Hz]')
ylabel('Phase [deg]')
grid on
set(gca,'XLim',[f(1) f(end)]) % 表示範囲の変更
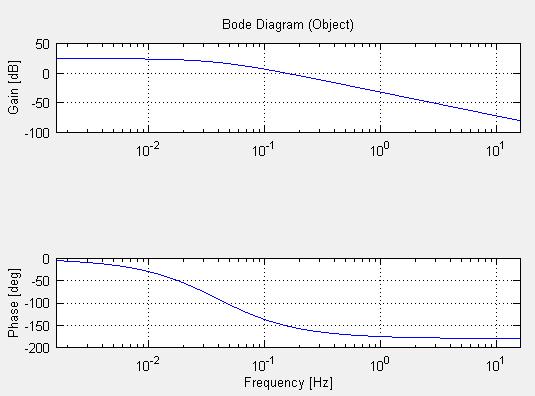Fig6-2 制御対象
（１）−３ 補償回路と組み合わせて、開ループ、閉ループのボード線図を書いてみます。
%補償回路
% Cs^2+Ds+E
% H(s)=------------
% s^2+As+B
A=0.84794
B=0.0004162
C=7.74731
D=1.40519
E=0.06121
sys1=tf2sys([C,D,E],[1,A,B]);
（１）−３−１ 補償回路と制御対象の直列結合（開ループ伝達特性）Fig6-3
%sys1とsys2の直列結合は sys = sysmult(sys1,sys2) で表せます。
sys3 = sysmult(sys1,sys2);
w = logspace(-2,2,100);
[mag,phase] = bode(sys3,w);
sysout(sys3);
subplot(2,1,1);
f = w/(2*pi); % rad/sec --> Hz
semilogx(f,20*log10(mag)); % ゲインの応答
title('Bode Diagram(Open loop)');
ylabel('Gain [dB]');
grid on
set(gca,'XLim',[f(1) f(end)]); % 表示範囲の変更
subplot(2,1,2);
semilogx(f,phase); % 位相の応答
xlabel('Frequency [Hz]');
ylabel('Phase [deg]');
grid on
set(gca,'XLim',[f(1) f(end)]) % 表示範囲の変更
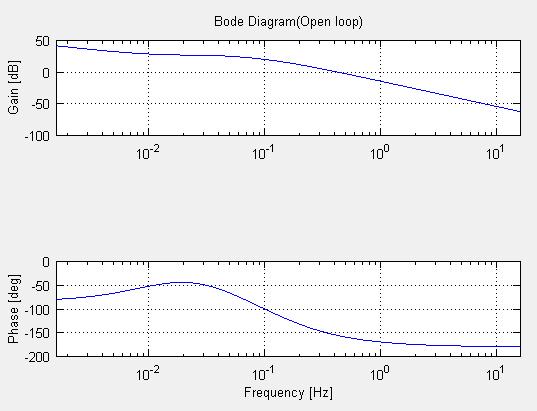Fig6-3
（１）−３−２ 閉ループ特性（負のフィードバック）Fig.6-4
% buildssic 関数を使います．
% sys = buildssic([1 -2;2 1],[],1,1,sys1,sys2)
% 引数の意味： [1 -2;2 1] sys1 にはsys2 の出力が負符号で入力される．
% sys2 にはsys1 の出力が入力される．この引数は行列として与える
% （要素数が不足する場合，0 で埋める）．
% 比例要素
% G(s) = K
% を設定するには sys = tf2sys(K,1); とする，
% 特に，G(s) = 1 に対しては
% sys = ugain(1);
%閉ループ伝達関数////////////////////////////////////////////////
sys4=ugain(1);
sys = buildssic([1 -2;2 1],[],1,1,sys3,sys4);
w = logspace(-2,2,100);
[mag,phase] = bode(sys,w);
figure(4);%/////////////////////////////////////////////////
subplot(2,1,1);
f = w/(2*pi); % rad/sec --> Hz
semilogx(f,20*log10(mag)); % ゲインの応答
title('Bode Diagram(Closed loop)');
ylabel('Gain [dB]');
grid on
set(gca,'XLim',[f(1) f(end)]) % 表示範囲の変更
subplot(2,1,2)
semilogx(f,phase) % 位相の応答
xlabel('Frequency [Hz]')
ylabel('Phase [deg]')
grid on
set(gca,'XLim',[f(1) f(end)]) % 表示範囲の変更
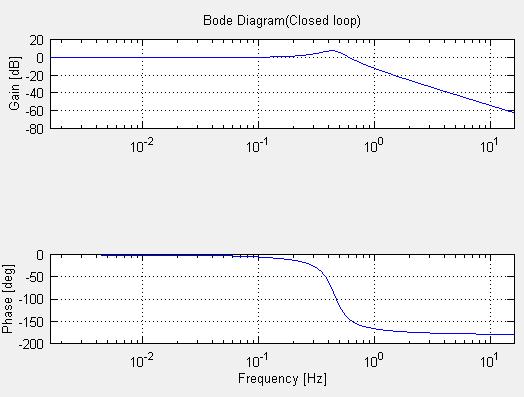Fig.6-4 Close loop
(2)オブザーバーを併合したレギュレータを構成（離散時間系）
%制御対象を離散化してみます
T=0.1;
Asys=ss2sys(Ac,Bc,Cc,Dc);
Dsys=c2d(Asys,T);% 0次ホールド、サンプリング時間Tで離散化
[A B C D]=sys2ss(Dsys);
%最適レギュレータのフィードバックゲインを計算します。
Q=[1 0;0 1];
R=[1];
[F P E]=dlqr(A,B,Q,R);%最適フィードバックゲインの計算
%dlqr：F(フィードバックゲイン)、P（リッカチ方程式の解：正定対称）
%E(閉ループ系の極、Ａ−ＢＦの固有値)
% 最適レギュレータの初期値応答 Fig.6-5
ft=8;
dt=0.001
n=ft/dt;
M=T/dt;
ic=0;
x=[1;1];%初期値
u=-F*x;
for i=1:n,
if ic==M
u=-F*x;
ic=0;
end;
xdot=Ac*x+Bc*u;
x=x+xdot*dt;
ic=ic+1;
y1(i)=x(1);
y2(i)=x(2);
tim(i)=i*dt;
um(i)=u;
end;
%/////////////////// figure(5)/////////////////////////////////////////
figure(5);
subplot(2,1,1)
plot(tim,um,tim,y1);
%um=input ,y1=output
title('Fig.6-5 Initial response(um(blue),y1(green)) Regulator ')
xlabel('time(sec)')
grid on
次にオブザーバーを併合してみます
n = 2;
A = A;
b = B;
c = C;
%d = [];
%sys = ss2sys(A,b,c,d);
sys = ss2sys(A,b,c);
Ao = A';%オブザーバーのAoはAの転置
bo = c';%オブザーバーのBoはｃの転置
co = eye(2,2);
%do = [];
%syso = ss2sys(Ao,bo,co,do);
syso = ss2sys(Ao,bo,co);
Pr = E; %Eは実軸に対称 レギュレータ極
Po = [0.95+0.05i 0.95-0.05i]; %オブザーバ極（指定値）離散時間系の極なので単位円の中にあること。すなわち絶対値は１未満
k = place(sys,Pr);%(A - kc) の固有値をPrに指定 レギュレータの極 フィードバックゲインkがもとまる
l = place(syso,Po);%(Ao - lc) の固有値をPoに指定 オブザーバーの極 フィードバックゲインｌがもとまる
l = l';
%オブザーバーで行う ここではxは推定値を表すただし、同一次元である
% simulation part
x=[0;0];%初期値
xr=[1;1];
%初期値
y=C*xr;
u=-F*x;
n=100;
for i=1:n
xn=A*x+B*u+l*(y-C*x);
xnr=A*xr+B*u;
xr=xnr;
x=xn;
y=C*xnr;
u=-F*x;
ym(i)=y;
timm(i)=i;
umm(i)=u;
end;
%/////////////////// figure(５-2)/////////////////////////////////////////
figure(5);
subplot(2,1,2)
plot(timm,umm,timm,ym);%blue line(1) green line(2)
%umm=input ,ym=output
title('Fig.6-6 Initial response(umm(blue), ym(green)) Observe+Regulator')
xlabel('time( * 0.1(sec))')
grid on
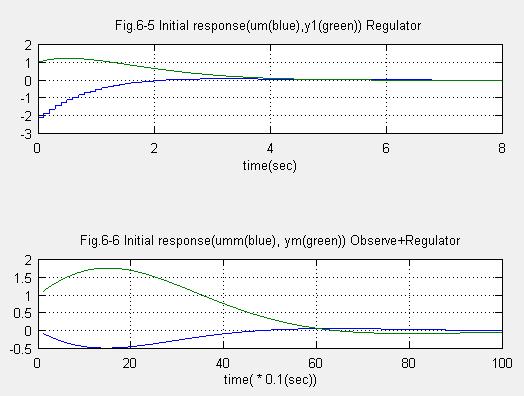Observer
こんな感じになるでしょうか
x=[0;0];%初期値
u=-F*x; %初期値
タイマー割り込み
y; %A/D読み込み
xn=A*x+B*u+l*(y-C*x);
x=xn;
u=-F*x;%制御入力
#pragma ioreg /* enable use the register directly in ca850 compiler */
#define ONE_SHOT 0 /* ワンショット・パルス用トリガ出力：1→有効/0→無効 */
#pragma interrupt INTTP2CC0 INTERVAL_Timer
extern unsigned long _S_romp;
unsigned char rto_cnt;
int p_x;
float duty;
unsigned int p_count;
float p_xn[3],p_yn[3],p_yout,p_xnad[5],p_ad;
/*───────────────────────────────────
* TMP2_Init Function(インターバルタイマモードで出力反転）
* ───────────────────────────────────
*/
void TMP2_Init(void)
{
TP2CE = 0; /* TP2CTL0.7：TMP2動作禁止 */
/* interrupt register setting */
TP2CCIC0 = 0x40; /* INTTP2CC0割込み優先レベル：0 */
/* timer register setting */
/* TP2CTL0 = 0x07; /* 内部カウント・クロック設定：fxx/512 */
TP2CTL0 = 0x06; /* 内部カウント・クロック設定：fxx/256 */
TP2CTL1 = 0x00; /* インターバル・タイマ・モード */
/* TP2CCR0 = (1000000*20/512) - 1; /* インターバル時間：1000ms(fxx/512設定) */
TP2CCR0 = (100000*20/256) - 1; /* インターバル時間：100ms(fxx/256設定) */
TP2CCR1 = 0xFFFF; /* 未使用 */
}
/*───────────────────────────────────
* TMP2_interrupt Function(インターバル割込み)
* ───────────────────────────────────
*/
__interrupt
void INTERVAL_Timer(void)
{
#if ONE_SHOT
PCM.0 ^= 1; /* ワンショット・パルス用トリガ信号反転 */
#else
PCT.6 ^= 1; /* LED1点滅（出力反転） */
#endif
p_count=0;
while (ADA0EF ==1 && p_count<50000 )
{ p_count++;
}
p_x=ADA0CR0; /* 上位１０ビットが有効 */
/* p_xn[0]=(float)((p_x>>6)-511); */
p_xn[0]=(float)((p_x>>6)-200);
p_ad += p_xn[0];
p_ad -= p_xnad[4];
p_xnad[4]=p_xnad[3];
p_xnad[3]=p_xnad[2];
p_xnad[2]=p_xnad[1];
p_xnad[1]=p_xn[0];
p_xn[0] = p_ad/5; /* ５ポイント移動平均 */
/* フィルタ係数は１００００倍している */
p_yn[0] =(19182.5*p_yn[1] - 9182.9*p_yn[2] + 74956.0*p_xn[0] - 148559.0*p_xn[1] + 73609.0*p_xn[2])/10000;
p_yout = p_yn[0]/5;
/* PWM 設定 */
duty = 50- (p_yout);
/* duty=50; */
if(duty>99){
duty=99;
}else if(duty<1){
duty=1;
}
/* TP3CCR1 =(int)(((25*20/1) * duty )/ 100); デューティ： %(TP3CCR0設定値 > TP3CCR1設定値) */
TP3CCR1 =(int)(5 * duty);
p_xn[2]=p_xn[1];
p_xn[1]=p_xn[0];
p_yn[2]=p_yn[1];
p_yn[1]=p_yn[0];
}
/*───────────────────────────────────
* TMP3_Init Function(PWM出力モード)
* ───────────────────────────────────
*/
void TMP3_Init(void)
{
TP3CE = 0; /* TP3CTL0.7：TMP3動作禁止 */
/* port register setting */
PFC9L.4 = 0; /* TOP31端子に設定(PWM出力) */
PFCE9L.4 = 1;
PMC9L.4 = 1;
PF9L.4 = 1; /* N-ch open drain */
/* timer register setting */
TP3CTL0 = 0x00; /* 内部カウント・クロック設定：fxx */
TP3CTL1 = 0x04; /* PWM出力モード */
TP3IOC0 = 0x04; /* TOP31出力許可 TOP31ハイ・アクティブ */
TP3CCR0 = (25*20/1) - 1; /* 周期：25us 40KHz */
TP3CCR1 = (25*20/1) * 50 / 100; /* デューティ： 50%(TP3CCR0設定値 > TP3CCR1設定値) */
/* TP3CCR0 = (1200*20/1) - 1; /* 周期：1200us */
/* TP3CCR1 = (1200*20/1) * 80 / 100; /* デューティ： 80%(TP3CCR0設定値 > TP3CCR1設定値) */
/* TP3CCR1 = (1200*20/1) * 0 / 100; /* デューティ： 0%(TP3CCR0設定値 > TP3CCR1設定値) */
/* TP3CCR1 = (1200*20/1) * 100 / 100; /* デューティ：100%(TP3CCR0設定値 > TP3CCR1設定値) */
}
/*───────────────────────────────────
* PORT_Init Function
* ───────────────────────────────────
*/
void PORT_Init(void)
{
/* port register setting */
#if ONE_SHOT
PCM.0 = 1; /* ロウ・アクティブのため */
PMCM.0 = 0; /* 出力ポートに設定 */
#else
PCT.6 = 1; /* ロウ・アクティブのため */
PMCT.6 = 0; /* 出力ポートに設定 */
#endif
}
/*───────────────────────────────────
* CPU_Init Function
* ───────────────────────────────────
*/
void CPU_Init(void)
{
VSWC = 1; /*システム・ウエイト・コントロール・レジスタ ウェイト数1 */
WDTM2 = 0; /* WDTM動作禁止 */
__asm("mov 0x00, r11");
__asm("st.b r11, PRCMD"); /* 特定レジスタを使用する前にPMCMDに書き込む */
__asm("st.b r11, PCC"); /* PCCの設定 PCC = 00: */
/* 周波数が安定するまで待つ */
while(LOCK); /* LOCK：1 アンロック状態，LOCK:0 ロック状態 */
SELPLL = 1; /* 1:PLL動作 0:PLL停止 */
}
/*───────────────────────────────────
* AD_Init Function
* ───────────────────────────────────
*/
void AD_init()
{
PM7L=0xFF; /* AN0 -- AN7 */
PM7H=0x0F; /* AN8 -- AN11 */
ADA0M0=0x22; /* ワンショット・セレクト,外部トリガ・モード／タイマ・トリガ・モード */
ADA0M1=0x81; /*高速 変換 時間 2.6 */
ADA0M2=0x01; /* タイマ・トリガ・モード0（INTTP2CC0割り込み要求発生時）*/
ADA0S=0x00; /* AN0 select */
ADA0PFM=0x00; /* パワー・フェイル比較モード・レジスタ（ADA0PFM）禁止 */
ADA0PFT=0x00; /* パワー・フェイル比較しきい値レジスタ（ADA0PFT）*/
ADA0S=0; /* AN0 */
}
/*───────────────────────────────────
* main Function
* ───────────────────────────────────
*/
void main(void)
{
int ret,n;
int msec;
p_xn[0]=0;
p_yn[0]=0;
p_xn[2]=p_xn[0];
p_xn[1]=p_xn[0];
p_yn[2]=p_yn[0];
p_yn[1]=p_yn[0];
p_yout=0;
p_ad=0;
p_xnad[0]=0;
p_xnad[1]=0;
p_xnad[2]=0;
p_xnad[3]=0;
p_xnad[4]=0;
/* CPU初期設定 */
CPU_Init(); /* CPU initiate */
AD_init();
/* ROM化処理 */
ret = _rcopy(&_S_romp, -1);
/* 周辺機能初期設定 */
PORT_Init(); /* PORT initiate */
TMP2_Init(); /* TMP2 initiate */
TMP3_Init(); /* TMP3 initiate */
ADA0M0.7=1; /* A/D変換動作許可 */
for( msec=0;msec<6000;msec++ )
{ __nop(); /* wait */
}
__EI();
/* タイマ動作許可 */
TP3CE = 1; /* PWM出力(TMP3)動作許可 */
TP2CCMK0 = 0; /* INTTP2CC0割込み許可 */
TP2CE = 1; /* インターバル・タイマ(TMP2)動作許可 */
while(1){
;
}
}